I m trying to do something like this:
Plot3D[x[s1, s2],
{s2, (m3^2 + m^2)^2, (Sqrt[s] - m^2)^2}, {s1,s1min[s2], s1max[s2]},
RegionFunction -> Function[{x[s1, s2]}, -1 < x < 1]]
but without success.
I m trying to do something like this:
Plot3D[x[s1, s2],
{s2, (m3^2 + m^2)^2, (Sqrt[s] - m^2)^2}, {s1,s1min[s2], s1max[s2]},
RegionFunction -> Function[{x[s1, s2]}, -1 < x < 1]]
but without success.
You can use ConditionalExpression using all the conditions that define the region you want to plot as the second argument:
ClearAll[x, m, m3, s1min, s1max]
x[s1_, s2_] := Sin[s1 + s2];
m = Sqrt[Pi/32];
m3 = Sqrt[Pi/64];
s1min[s_] := Sqrt@s;
s1max[s_] := 2 + Sqrt@s;
Plot3D[ConditionalExpression[x[s1, s2],
(m3^2 + m^2)^2 <= s2 <= (Sqrt[s1] - m^2)^2 &&
s1min[s2] <= s1 <= s1max[s2] && -1 < x[s1, s2] < 1],
{s1, 0, Pi}, {s2, 0, Pi}, PlotPoints -> 100, MaxRecursion -> 4]
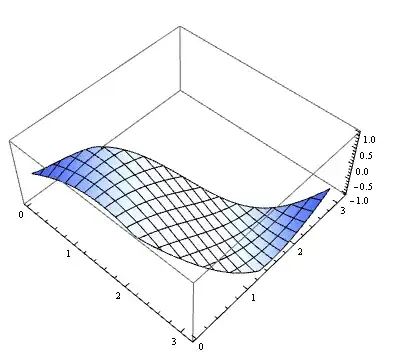
or, use RegionFunction
Plot3D[x[s1, s2], {s1, 0, Pi}, {s2, 0, Pi}, PlotPoints -> 100, MaxRecursion -> 4,
RegionFunction ->
Function[{s1, s2, z}, (m3^2 + m^2)^2 <= s2 <= (Sqrt[s1] - m^2)^2 &&
s1min[s2] <= s1 <= s1max[s2] && -1 < z < 1]]
(* same picture *)
s1ands2have to be constants, and your syntax forFunctionis wrong. Try integrating the conditions ons1into theRegionFunction, something likeFunction[{s1, s2, x}, -1 < x < 1 && s1min[s2] < s1 < s1max[s2]]. – 2012rcampion Mar 27 '15 at 00:09