NDSolve Poisson PDE for rectangle with hole

Question

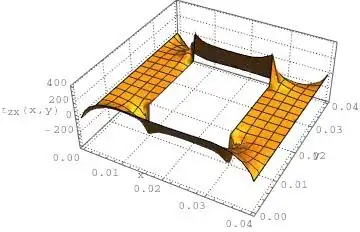
When I solved the Poisson PDE with function NDSolve in a rectangular domain with hole in the center, and search the first derivative with x and y why appear these protrusions on the diagram around the hole?

And how to draw wectorfield with wectorplot on a rectangle, which have a hole inside? Thanks for help.

G = 13.5 10^6;
θ = 0.002;
n = 5;
m = 5;
Ω = 
RegionDifference[Rectangle[{0, 0}, {0.04, 0.04}], 
Rectangle[{0.01, 0.01}, {0.03, 0.03}]];
sol = NDSolveValue[{D[u[x, y], x, x] + 
  D[u[x, y], y, y] == -2 G θ, 
DirichletCondition[u[x, y] == 0., 
 x == 0.01 && 0.01 <= y <= 0.03 || 
  x == 0.03 && 0.01 <= y <= 0.03 || 
  0.01 <= x <= 0.03 && y == 0.01 || 
  0.01 <= x <= 0.03 && y == 0.03], 
u[x, 0] == u[x, 0.04] == u[0, y] == u[0.04, y] == 0}, 
u, {x, y} ∈ Ω, 
Method -> {"FiniteElement", 
 "MeshOptions" -> {"BoundaryMeshGenerator" -> "Continuation"}}];
Subscript[τ, yz] = -D[sol[x, y], x];
Subscript[τ, xz] = D[sol[x, y], y];
Plot3D[sol[x, y], {x, y} ∈ Ω, 
PlotStyle -> None, Mesh -> True, PlotRange -> All, 
AxesLabel -> {"x", "y", "ϕ(x,y)"}, PlotTheme -> "Detailed", 
LabelStyle -> Directive[FontFamily -> "Courier New"]]
Plot3D[Subscript[τ, yz], {x, y} ∈ Ω, 
PlotStyle -> None, PlotTheme -> "Detailed", Mesh -> True, 
AxesLabel -> {"x", "y", 
"\!\(\*SubscriptBox[\(τ\), \(zy\)]\)(x,y)"}, 
LabelStyle -> Directive[FontFamily -> "Courier New"]]
Plot3D[Subscript[τ, xz], {x, y} ∈ Ω, 
PlotTheme -> "Detailed", Mesh -> True, 
AxesLabel -> {"x", "y", 
"\!\(\*SubscriptBox[\(τ\), \(zx\)]\)(x,y)"}, 
LabelStyle -> Directive[FontFamily -> "Courier New"]]
VectorPlot[{Subscript[τ, xz], Subscript[τ, yz]}, {x, 0, 
0.04}, {y, 0, 0.04}, PlotRange -> All, Axes -> True, 
AxesLabel -> {x, y}, 
LabelStyle -> Directive[FontFamily -> "Courier New"]]

Answer 1

The solution for this is to update to a newer version. V10.0.2 fixed the issues, so that version or any later one will do.

Running the above code with

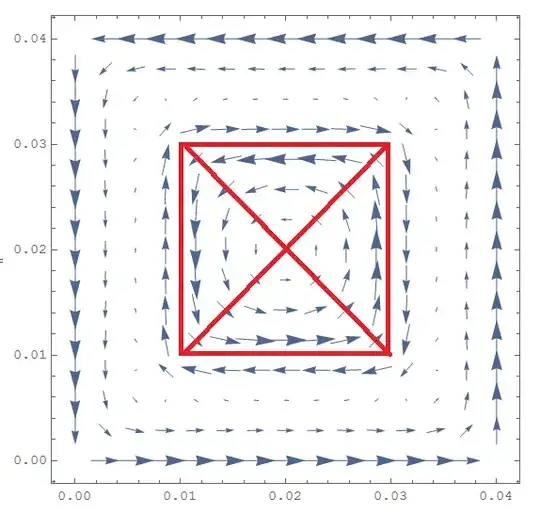
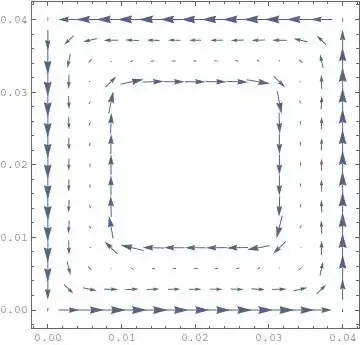
VectorPlot[{Subscript[\[Tau], xz], 
  Subscript[\[Tau], yz]}, {x, y} \[Element] \[CapitalOmega], 
 PlotRange -> All, Axes -> True, AxesLabel -> {x, y}, 
 LabelStyle -> Directive[FontFamily -> "Courier New"]]

The gives the vector plot:

And the plot looks like: