It's pretty clear that the complexity of this function is $\text{O}(n^3)$, since we're iterating over each element of a matrix (a factor of $n^2$) and taking a sum at each one (an additional factor of $n$). However, we can't really do anything to reduce the complexity; LU decomposition has the same complexity as matrix multiplication. Although algorithms faster than $\text{O}(n^3)$ do exist I do not think they are used in practice.
The upshot of all this is that if we really want to increase our speed, we should Compile our function. Here is an algorithm in Fortran that is in-place; that is, it doesn't use any extra memory (although we do need to copy the matrix once so that we can 'edit' it). We can write a CompiledFunction to implement this version of the algorithm:
doolittleDecomposition = Compile[{{a, _Real, 2}},
With[{n = Length[a]},
Module[{t = a},
Do[
Do[
Do[
t[[i, j]] -= t[[i, k]] t[[k, j]];,
{k, 1, i - 1}];,
{j, i, n}];
Do[
Do[
t[[j, i]] -= t[[j, k]] t[[k, i]];,
{k, 1, i - 1}];
t[[j, i]] /= t[[i, i]];,
{j, i + 1, n}];,
{i, 1, n}];
t
]
],
{{q, _Real}}
, RuntimeOptions -> {"Speed", "EvaluateSymbolically" -> False},
CompilationTarget -> "C",
CompilationOptions -> {"ExpressionOptimization" -> True}]
We should double-check that our function doesn't call MainEvaluate, which is slow:
Needs["CompiledFunctionTools`"]
doolittleDecomposition // CompilePrint
While doing this check I discovered that I originally wrote t[j, i] instead of t[[j, i]], causing MainEvaluate to be called. Always double-check! In fact, let's now double-check that both algorithms give the same result:
testReal = RandomReal[1, {200, 200}];
d1 = doolittleDecomposite[testReal]; // AbsoluteTiming
d2 = doolittleDecomposition[testReal]; // AbsoluteTiming
d1 == d2
This also shows that the Compiled version is faster.
Update: Refactoring the original code
If you think Compile is too drastic (or you don't have a working C compiler) there are some other changes we can make.
- Don't use an auxiliary or 'helper' function. This will incur extra overhead that you don't need. Unlike a compiled language where the compiler will essentially inline the function, Mathematica will be passing-by-value all of your matrices!
- Don't use
Nest. If we're getting rid of the helper function, Nest doesn't really make sense. We can replace it with a Do-loop instead. The Do-loop can 'automatically' increment k, instead of having to pass it (in a list!) to a function and have it returned (also in a list!!). At this point we can rename intermediate to temp, consolidating two variables that really contain the same thing, and we also can lose the extra redefinition of row inside the loop.
- Use
Dot instead of Sum. In general, if there's a builtin function for something, that function is faster. In this case you want to pairwise multiply two lists and take the sum of the resulting elements. We usually call that a dot product. Instead of looping m, we can use Span to extract a list using Part, and then Dot our two lists together. This is where most of the speedup comes from.
At this point the code looks pretty much like the Fortran function, but with the inner loops handled by Dot:
doolittleDecomposite2[mat_?MatrixQ] :=
Module[{temp = ConstantArray[0, Dimensions@mat], row = Length@mat},
Do[
Do[temp[[k, j]] =
mat[[k, j]] - temp[[k, ;; k - 1]].temp[[;; k - 1, j]],
{j, k, row}];
Do[temp[[i, k]] =
(mat[[i, k]] - temp[[i, ;; k - 1]].temp[[;; k - 1, k]]) / temp[[k, k]],
{i, k + 1, row}];,
{k, row}];
temp
]
Updated performance analysis
I ran another comparison, this time including LUDecomposition, just to see how well we did:

The first thing I noticed (even before I generated the plots) was that the original solution takes an unreasonably long time on matrices larger than around $n>250$ (I tried $n=400$ and let it run for at least an hour before aborting manually). I suspect this has to do with memory bandwidth when passing temp into Sum.
The second think to notice is that LUDecomposition is fast. Not only is it at least two orders of magnitude faster than mine, but below $n=1000$ it is almost instant (less than 10 ms). The former is probably from using highly optimized libraries like the the Intel MKL. As for the latter, it's probably not a coincidence that the 'fast' runs all have memory usage below the size of my CPU cache (8MB):
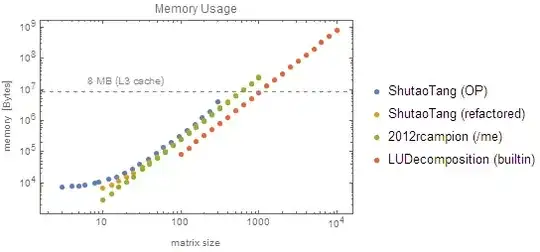
The third thing to notice is that while all of our solutions are firmly $\text{O}(n^3)$ for large numbers, the native LUDecomposition is actually closer to $\text{O}(n^{2.4})$, meaning that there is probably a large $\text{O}(n^2)$ factor that the leading $n^3$ won't dominate until very large $n$.
Similarly, although the refactored version appears to be slightly better than $\text{O}(n^3)$, this is only because of all the overhead; as the vectors passed to Dot get larger, the $n^3$ term will eventually dominate.
Looking back at the memory usage plot, we can see that the original function doesn't use much more memory than mine. All are asymptotically $\text{O}(n^2)$. The reason the original takes so long is because Mathematica is essentially pass-by-value, so it's making a huge malloc and free every time it calls the helper function.
The refactored version uses almost exactly the same amount of memory as my Compiled solution (excepting a small $\text{O}(n)$ contribution from the vectors and Dot) because we avoid all that argument-passing and copying.
As to why I'm using almost exactly 3× more memory than LUDecomposition, it's probably also due to pass-by-value semantics: Mathematica constructs a version of the matrix to pass to the CompiledFunction, which then makes it's own working copy, which is then copied again to produce the result. As LUDecomposition is a native function, it can avoid all that.


Tableprobably should beDo. For the machine real case you could run it throughCompile. – Daniel Lichtblau Mar 31 '15 at 16:05oneStepfunction that I implemented is C-style(like procedural paradigm) . So my main difficult ishow to store and organize the intermediate result in right wayif I'd like to implement this algorithm with functional or rule-based paradigm. – xyz Apr 03 '15 at 05:21Reverse[IdentityMatrix[4]]. As for pivoting: did you notice the difference between your method andLUDecomposition[]? The latter one outputs a permutation list, which encodes the (partial) pivoting (interchanges of rows) done in the course of decomposing the matrix. Any robust implementation has to have a pivoting strategy like that. – J. M.'s missing motivation Oct 24 '15 at 11:55Reverse[IdentityMatrix[4]] // doolittleDecomposite2in this answer gives thePower::infyerror information. And I noticed the difference thatLUDecompositionreturns a list of three elements. – xyz Oct 24 '15 at 12:31LUdecomposition came from my textbook of Numerical Analysis. – xyz Oct 24 '15 at 12:39