I have two functions defined on the same domain, $f(x)$ and $g(x)$ where $x$ is in $(0,1)$:
f[x_] := (-1 + x) Log[1 - x] - x Log[x]
g[x_] := Log[1 + 2 (-1 + x) x]
I would like to find a constant $c$ such that the maximum of $f(x)-cg(x)$ is minimized on the domain $(0,1)$.
My first attempt was to try
Minimize[Maximize[{f[x]-c g[x],0<x<1},x],c]
but this just gives me back my input as the output.
Am I going about this the wrong way entirely? I feel like it's got something to do with the inner Maximize not evaluating because it's a function of more than one variable but I have no idea how to deal with this.
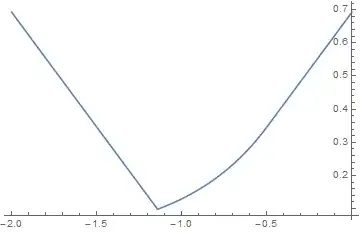
 From playing with it it becomes clear that the minimum value of the function
From playing with it it becomes clear that the minimum value of the function 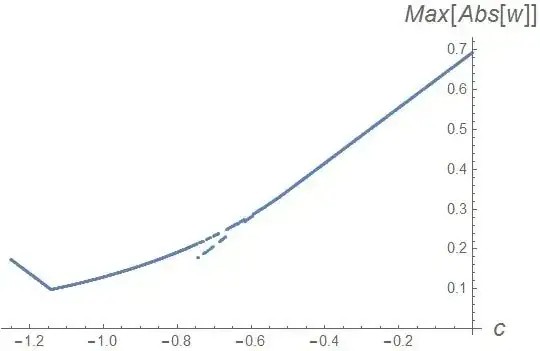
cappropriately, even for these functions. However your question is still unclear. Do you want to minimize pointwise $f(x)-cg(x)$ or in a different norm? – Artes Apr 01 '15 at 13:30Plot[Maximize[{f@x - c g@x, 0 < x < 1}, x][[1]], {c, -5, 1}]– Dr. belisarius Apr 01 '15 at 13:37@usrname, otherwise the other user isn't notified – Dr. belisarius Apr 01 '15 at 13:38MaxValueinstead ofMaximize[[1]](seeing as you're going for brevity withf@xand all) – 2012rcampion Apr 01 '15 at 13:46f[x]-c g[x]? – Alexei Boulbitch Apr 01 '15 at 14:15