How can I create a phase plane?

Question

I want to make a phase plane for an equation system. I want it to look something like a Mu-Space in Stat-Mech. Basically I want it to show the same system with various different initial condition pairs {C(0), N(0)} and show how the system evolves as an {C[t], N[t]} pair. I would like to have these different systems plotted on the same plane. Unfortunately I am not well equipped to deal with this sort of thing. The code I have right now is below:

(*Constants*)
s = .1;
g = 1;
a = .75;
p = 30;
da = .1;
alpha = .01;
beta = 1;
k = 10000;
deltaP = 10;

(*Algebraic*)
Pn = deltaP/10000;
f[t_] = 1 - 1/(a*Ca[t] + 1);
(*ODE system*)
solution = 
 NDSolve[{Ca'[t] == s*(p + Pn*Na[t])*f[t] - (g + da)*Ca[t], 
   Na'[t] == alpha + beta/k*Na[t]*(k - Na[t]), Ca[0] == 1, 
   Na[0] == 1}, {Ca, Na}, t]

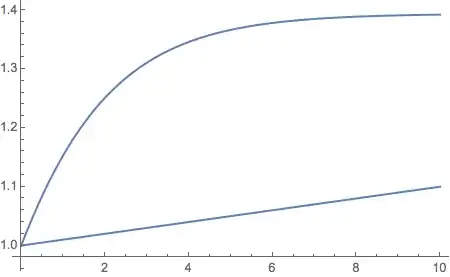
Plot[Evaluate[{Na[x], Ca[x]} /. solution], {x, 0, 10}, 
 PlotRange -> All]

I would like to be able to turn this code into something similar to what I described above. Any assistance is appreciated.

Edit

I have been trying to use Equation Trekker from the linked material. I am unsure what mistake I am making.

EquationTrekker[
  Ca'[t] == s*(p + Pn*Na[t])*f - (g + da)*Ca[t], 
  Na'[t] == alpha + beta/k*Na[t]*(k - Na[t]), 
  Na[t], {Ca[t], 0, 10}]

Edit2

Also, Using the parametric plot code listed in one of the responses

ParametricPlot[Evaluate[{nn[t], cc[t]} /. solution], {t, 0, 10}, AspectRatio -> 1/2]

I now have a plot of C vs N for one set of initial conditions. I don't know what the best way to get multiple such plots with different intial conditions. I have also fixed my variable names in the body of my code.

Answer 1

With the constants you've given, try the following code for the solution steps

(*Algebraic*)
Pn = deltaP/10000;
f[t_] := 1 - 1/(a*cc[t] + 1);
(*ODE system*)
solution = First@NDSolve[
   {cc'[t] == s*(p + Pn*nn[t])*f[t] - (g + da)*cc[t],
    nn'[t] == alpha + beta/(k*nn[t]*k - nn[t]),
    cc[0] == 1,
    nn[0] == 1},
   {cc[t], nn[t]},
   {t, 0, 10}
   ]

This will produce two InterpolationFunctions. Note that C and N are built in Mathematica commands. One way to avoid conflicts between you own variables and built-in commands is to begin your own variable names with small letters.

Note also that when you use ReplaceAll, you have to use cc[t] and nn[t] exactly so the pattern for replacement matches the rules in solution.

You can do a standard plot with t on the horizontal axis

Plot[{nn[t], cc[t]} /. solution, {t, 0, 10}, PlotRange -> All]

And if you want a phase plot where the two variables cc and nn are plotted against each other, you can use ParametricPlot.

ParametricPlot[Evaluate[{nn[t], cc[t]} /. solution], {t, 0, 10}, AspectRatio -> 1/2]

Although you can implement loops in a procedural style in Mathematica, it is generally better (eg. more efficient, cleaner code, ...) to use Mathematica's inherent Functional Programming nature.

So here you might use Table to generate a List of multiple solutions.

solutions = 
  Table[NDSolve[{cc'[t] == s*(p + Pn*nn[t])*f[t] - (g + da)*cc[t], 
     nn'[t] == alpha + beta/(k*nn[t]*k - nn[t]), cc[0] == i, 
     nn[0] == j}, {cc[t], nn[t]}, {t, 0, 10}],
   {i, {1, 1.2, 1.5}},
   {j, {1, 1.2, 1.5}}
   ];

Then Flatten this list of Rules in the first argument to ParametricPlot, which can be a List of functions.

ParametricPlot[
  Evaluate[{nn[t], cc[t]}] /. Flatten[solutions, 2],
  {t, 0, 10}, 
  AspectRatio -> ½
  ]