1

Can you suggest me a simple way to specify custom display format (for example ScientificForm) for such large values in contour labels and legend please?

Thank you!

k = 1.380648813 10^-23;(* Boltzmann constant*)

ContourPlot[1/(k T )  Log10[1 + Z]/Z,
 {T, 273, 330},
 {Z, 1, 50},
 ImageSize -> Large,
 FrameLabel -> {{"\!\(\*
StyleBox[\"Z\",\nFontSlant->\"Italic\"]\)", None}, {"\!\(\*
StyleBox[\"T\",\nFontSlant->\"Italic\"]\)\!\(\*
StyleBox[\",\",\nFontSlant->\"Italic\"]\)\!\(\*
StyleBox[\" \",\nFontSlant->\"Italic\"]\)\!\(\*
StyleBox[\"K\",\nFontSlant->\"Italic\"]\)", None}}, 
 LabelStyle -> {GrayLevel[0], Bold},
 Contours -> Automatic,
 ContourLabels -> Automatic,
 PlotLegends -> Automatic
 ]

contour plot with large numbers

Andrey Kazak
  • 15
  • 1
  • 5
  • Could you please provide code of above example, in order to permit the community to answer effectively ? – penguin77 Apr 03 '15 at 20:57
  • 1
    Why not simply define a new function to be $10^{-18}$ your current function? – David G. Stork Apr 03 '15 at 21:52
  • I added the code. I cannot multiply the function by 10−18 because this multiplier can change by orders of magnitude. That is I want number format to be automatically adjusted in every case. – Andrey Kazak Apr 04 '15 at 02:27

2 Answers2

3

Replace PlotLegends -> Automatic by

PlotLegends -> BarLegend[Automatic, 
  LabelingFunction -> (Style[NumberForm[#, {Infinity, 3}], Bold, Black, 12] &)]

to produce

enter image description here

Many other formats are possible, depending on what you are seeking. (By the way, just ignore that LabelingFunction is in red in Mathematica. It works anyway.)

Addendum

In answer to the question in the comment below, I suggest the following:

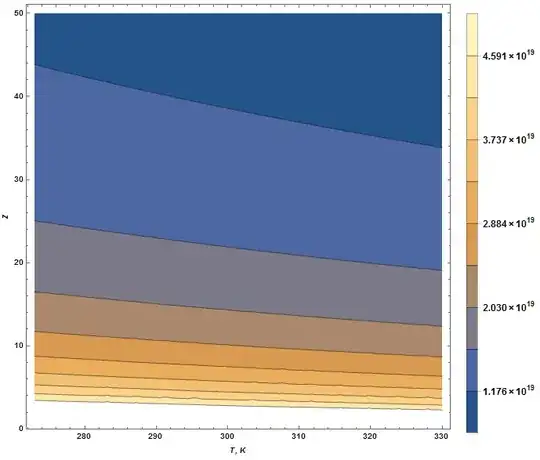
k = 1.380648813 10^-23;(*Boltzmann constant*)
T1 = 273; T2 = 330; rs = .1;
plt = ContourPlot[rs/(k T) Log10[1 + Z]/Z, {T, T1, T2}, {Z, 1, 50}, 
  ImageSize -> Large, FrameLabel -> {Style["T, K", Italic], Style["Z", Italic]}, 
  LabelStyle -> {Black, Bold, 12}, PlotRange -> All, 
  ContourLabels -> Function[{x, y, z}, 
    Inset[Style[NumberForm[N[z/rs], {Infinity, 1}], Bold, 12], 
      {Piecewise[{{x + 3, x < T1 + 3}, {x - 3, x > T2 - 3}}, x], y}]], 
  PlotLegends -> BarLegend[Automatic, LabelingFunction -> 
    (Style[NumberForm[N[#/rs], {Infinity, 1}], Bold, Black, 12] &)]]

Unfortunately, it includes two "work-arounds". First, a temporary rescaling, rs has been added to take account that ContourPlot does not pass ContourLabels of 10^19 or greater. I shall look further into this idiosyncrasy. Second, a Piecewise function has been added to better center the ContourLabels.

Additionally, PlotRange -> All has been added to recover the small portion of plot at the bottom and to improve the accuracy of the BarLegend labels. Labeling format also has been improved.

enter image description here

Second Addendum

As an alternative to adjusting the positions of ContourLabels for better centering, they can be allowed to extend outside the frame with the code

k = 1.380648813 10^-23;(*Boltzmann constant*)
T1 = 273; T2 = 330; rs = .1;
plt = ContourPlot[rs/(k T) Log10[1 + Z]/Z, {T, T1, T2}, {Z, 1, 50}, 
  ImageSize -> Large, FrameLabel -> {Style["T, K", Italic], Style["Z", Italic]}, 
  LabelStyle -> {Black, Bold, 12}, PlotRange -> All, 
  ImagePadding -> All, PlotRangeClipping -> False,
  ContourLabels -> Function[{x, y, z}, 
    Inset[Style[NumberForm[N[z/rs], {Infinity, 1}], Bold, 12], {x, y}]], 
  PlotLegends -> BarLegend[Automatic, LabelingFunction -> 
    (Style[NumberForm[N[#/rs], {Infinity, 1}], Bold, Black, 12] &)]]

Alternatively, the frame can be made larger by replacing ImagePadding -> All, PlotRangeClipping -> False, by PlotRangePadding -> 3.2,.

Third Addendum

Jens' answer to Question 79052 can be used to eliminate the first "work-around" described above. 

k = 1.380648813 10^-23; t1 = 273; t2 = 330; z1 = 1; z2 = 50;
f[t_, z_] := 1 Log10[1 + z]/(k t z)
plt = ContourPlot[f[t, z], {t, t1, t2}, {z, z1, z2}, 
  ImageSize -> Large, FrameLabel -> {Style["T, K", Italic], Style["Z", Italic]}, 
  LabelStyle -> {Bold, Black, 12}, PlotRange -> All,
  ContourLabels -> (Inset[Style[NumberForm[f[#1, #2], {Infinity, 1}], Bold, 12], 
        {Piecewise[{{#1 + 3, #1 < t1 + 3}, {#1 - 3, #1 > t2 - 3}}, #1], #2}] &), 
  PlotLegends -> BarLegend[Automatic, 
    LabelingFunction -> (Style[NumberForm[#, {Infinity, 1}], Bold, Black, 12] &)]]

which yields a plot identical to the second one above. A Comment by Simon Woods in Question 79052 also provides an alternative.

Community
  • 1
bbgodfrey
  • 61,439
  • 17
  • 89
  • 156
3

Replace PlotLegends-> Automatic with Barlegend combined with option LegendFunction

PlotLegends -> 
  BarLegend[Automatic, LegendFunction -> (ScientificForm[# // N] &)]]

enter image description here

penguin77
  • 1,645
  • 9
  • 8