How do I map a function onto the result of an expression that already has a pure function as an argument

Question

I admit that I have only a basic understanding of the way Mathematica handles pure functions - enough to be dangerous, unfortunately.

I have some data that is in a list of lists of lists. I would like to apply a function over a subset of each of those (top level) lists, and I'm wondering if there is a way to do it with mapping rather than using Table. In the following example I have three lists of ordered pairs. I'd like to quickly select a subset of each of those three top level lists by testing a property of the deepest level elements. Doing it for one of the three is easy:

testList = Table[Table[{i, RandomReal[]}, {i, 100}], {j, 1, 3}];
subset1 = Select[testList[[1]], PrimeQ[#[[1]]]&];

What I'm wondering is whether or not there is some way to do something like this:

subsetList = Select[<argument>, PrimeQ[#[[1]]]&] & /@ testList

where "argument" is some sort of indicator that it should be mapped "outside" to the testList level. I'm sure there's some obvious use of Apply or some such that can do this, I just can't quite figure it out!

I don't know if those are good enough to be duplicates: 16947, 35322. — Kuba, Apr 09 '15 at 05:59
This works, but I certainly did not think it would until you suggested it. I guess it's because each "&" denotes a separate rule? If you can help me understand why this works and doesn't confuse the "#"s I'd appreciate it. I'm accepting a slightly different answer since it seems more general. — djphd, Apr 09 '15 at 19:25

score 5 · Accepted Answer · answered Apr 09 '15 at 03:10

5

Use the pure function in the form of Function[x, ...] or Function[{x, y}, ...] for more arguments. For example,

Function[arg, Select[arg, PrimeQ[#[[1]]] &]] /@ testList

answered Apr 09 '15 at 03:10

Taiki

5,259
26
34

1

This not only works, but is also easily readable and parse-able by my tiny coding brain. Thanks! – djphd Apr 09 '15 at 19:29

score 1 · Answer 2 · answered Apr 09 '15 at 03:58

Here is another way using Cases

 Cases[#, {x_, y___} /; PrimeQ[x] :> {x, y}] & /@ testList

Versification with Map method given by Taiki

testList = Table[Table[{i, RandomReal[]}, {i, 10}], {j, 1, 3}];
Function[arg, Select[arg, PrimeQ[#[[1]]] &]] /@ testList
Cases[#, {x_, y___} /; PrimeQ[x] :> {x, y}] & /@ testList

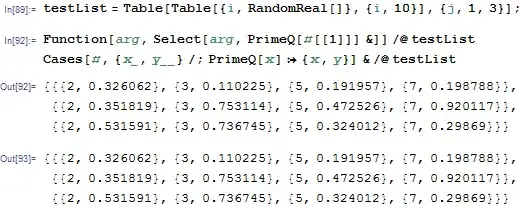
Mathematica graphics

score 1 · Answer 3 · answered Apr 09 '15 at 11:21

Just to illustrate (using testList definition given) :

c1 = Cases[#, {_?PrimeQ, _}, Infinity] & /@ testList;
c2 = Select[#, PrimeQ[First@#] &] & /@ testList;
c3 = Pick[#, Map[Function[x, PrimeQ[First@x]], #]] & /@ testList;

and for the ridiculous:

c4 = Flatten[Last[Reap[Sow[{##}, #1], _?PrimeQ, #2[[1]] &]]] /. {} -> 
        Sequence[] & @@@ # & /@ testList;

Note:

And[c1 == c2, c2 == c3, c3 == c4]

yields True

How do I map a function onto the result of an expression that already has a pure function as an argument

3 Answers3

Linked