Finding the intersection of two graphs

Question

I'm having difficulty with finding the intersecting point of two graphs. Here is what I have done so far:

Plot[{8*n^2, 64*n*Log2[n]}, {n, 0, 100}]

which produces the following graph:

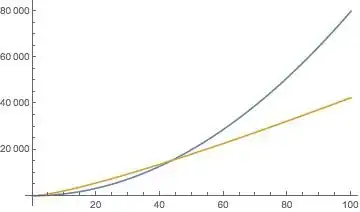
enter image description here

To find the intersection I tried:

FindRoot[{8*n^2, 64*n*Log2[n]}, {0, 100}, {0, 20000}]

But I got an error I think:

FindRoot::nlnum1: "The function value {{8.\ n^2,92.3325\ n\ Log[n]}[0.,0.]} is not a list of numbers with dimensions {1} when the arguments are {0.,0.}"

I am using Mathematica 10.

Solve[8*n^2 - 64*n*Log2[n] == 0, n] // N – Dr. belisarius Apr 09 '15 at 14:14 — Dr. belisarius, Apr 09 '15 at 14:14
I'm sorry, have you seen FindRoot documentation page? – Kuba Apr 09 '15 at 14:15 — Kuba, Apr 09 '15 at 14:15
Possible duplicate of 74150 or 28987. – dionys Apr 09 '15 at 14:35 — dionys, Apr 09 '15 at 14:35

dionys · Answer 1 · 2015-04-09T14:43:42.233

1

One approach is to set the first equation equal to the second and use Reduce to solve the system:

Block[{f1, f2, n, sol},
 f1 := 8*n^2;
 f2 := 64*n*Log2[n];
 sol = N@Reduce[f1 == f2, n]]

(* n == 1.1 || n == 43.5593 *)

Also, you might want to check out the Mathematica tutorials on equation solving.

edited Apr 09 '15 at 14:43

answered Apr 09 '15 at 14:19

dionys

4,321
1
19
46

Finding the intersection of two graphs

1 Answers1

Linked