1

The specific type of system looks as follows:

\begin{align} (r-r')x+4d_1 x^3+4d_{12}xy^2 &= 0 \\ (r+r')y+4d_2 y^3+4d_{12}yx^2 &= 0 \\ \end{align} Where $r,r',d_1, d_2, d_{12}$ are all real parameters and all the $d$ type parameters follow the condition $d>0.$ Now since the system at hand has so many parameters, one may be interested in different scenarios of parameters, e.g. when $r,r'$ are both $0$ and so on. So I thought best would be to go for a graphical solution, using manipulate on all parameters. Admittedly I do not have much experience with such computations, but anyhow here are my two main attempts, first trying analytic solutions:

$Assumptions = {(r | r' | d1 | d2 | d12) \[Element] Reals && (d1 | d2 | d12) > 0 && d1 d2 > d12^2 }

equations = { (r-r') x + 4 d1 x^3 + 4 d12 x y^2 == 0, (r+r') y + 4 d2 y^3 + 4 d12 y x^2 == 0};

Then using Simplify[Reduce[equations, {x, y}]] gives a page of long analytic solutions with Root and seems to ignore my assumptions, and I cannot get it to simplify the expressions further (at the cost of having not exact Root solutions anymore).

Second attempt, a graphical one:

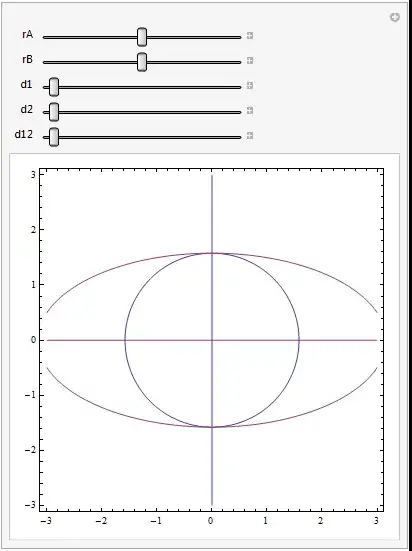
Manipulate[ ContourPlot[equations, {x, -10, 10}, {y, -10, 10}, PlotPoints -> ControlActive[10, 50], MaxRecursion -> ControlActive[1, 10]], {r, -2, 2}, {r', -2, 2}, {d1, 0, 10}, {d2, 0, 10}, {d12, 0, 10}]

Such approach would be preferential as one would then really be able to play with the parameters and learn all about the system and its solutions (e.g. how many of them etc). But I don't know if the contourplot is a good idea because I can't make any sense of the results yet, added to which it is a bit difficult to guess the right range of values for the variables and parameters.

  • Can anyone come up with suggestions that can improve any of the two attempts?
  • 1
    This might give a result more to your liking (maybe). `equations = {(r - rp) x + 4 d1 x^3 + 4 d12 x y^2 == 0, (r + rp) y + 4 d2 y^3 + 4 d12 y x^2 == 0, Element[{r, rp}, Reals], d1 > 0, d2 > 0, d12 > 0, d1 d2 > d12^2};

    result = Reduce[equations, {x, y}, Reals]`

     – Daniel Lichtblau Apr 20 '15 at 15:31
  • @DanielLichtblau Thanks a lot for the modified suggestion, a lot better now. In the results what do the two parallel bars stand for? –  Apr 22 '15 at 10:06
  • That's the sort of thing documentation is really good for (and this forum is not. – Daniel Lichtblau Apr 22 '15 at 13:11

1 Answers1

1

For a graphical study I would solve the two equations independently. First one gives you one up to three x-solutions with y as additional parameter. Second one give one up to three y-solutions with x as additional parameter. Next I would plot the solutions as ParametricPlot[] with different colors on top of each other.

So something like

solx=Solve[(rA-rB) x + 4 d1 x^3 + 4 d12 x y^2 == 0,x];
soly=Solve[(rA+rB) y + 4 d1 y^3 + 4 d12 y x^2 == 0,y];

xx[i_][t_,{rA_,rB_,d1_,d2_,d12_}]:=Evaluate[solx[[i,-1,-1]] ];
yy[i_][t_,{rA_,rB_,d1_,d2_,d12_}]:=Evaluate[soly[[i,-1,-1]] ];

Manipulate[
ParametricPlot[
{
    Table[{xx[i][t,{rA,rB,d1,d2,d12}],t},
    {i,3}],
    Table[{t,yy[i][t,{rA,rB,d1,d2,d12}]},
    {i,3}]
},{t,-3,3}],
{{rA,-1},-2,0},
{{rB,-1},-2,2},
{{d1,.1},0,10},
{{d2,.1},0,10},
{{d12,.1},0,10},
]

Providing this animation

But this is probably too much for the problem at hand. It is clear that the first equation always has x=0 as solution. Likewise y=0 solves the second. The remaining equations give an ellipse. Just plot the ellipses and you have it as well.

Community
  • 1
mikuszefski
  • 4,877
  • 1
  • 14
  • 18
  • I get some error messages upon defining xx and yy. Don't know why, but as it works I don't care too much. – mikuszefski Apr 16 '15 at 13:18
  • 1
    Good idea! There seems to be few syntax errors in there, e.g. you're missing a comma in Table[{xx[i][t,{rA,rB,d1,d2,d12}],t} {i,3}] , a comma too much at the end of {{d12,.1},0,10}, ], finally the second equation should probably be (following OP's equations) soly=Solve[(rA+rB) y + 4 d1 y^3 + 4 d12 y x^2 == 0,y]; – Ellie Apr 16 '15 at 14:58
  • @Phonon Thanks for mentioning. Edited. – mikuszefski Apr 16 '15 at 15:26
  • My pleasure, it's a good answer. – Ellie Apr 16 '15 at 15:33