Nearest neighbor distribution

Question

I need to construct nearest neighbor distribution for a given finite set of real numbers. I have no clue how this can be realized. Any suggestion would be very much appreciated.

Answer 1

Expanding on David's answer, this will be vastly faster on larger lists:

With[{nf = Nearest[#]},EuclideanDistance[Last@nf[#, 2], #] & /@ #] &@myList

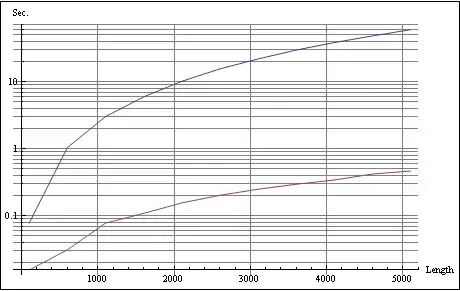
For even faster results (e.g., on a list of 100K reals, this is ~250X faster than mine above, don't know how much faster than David's, I'd imagine many orders of magnitude):

newF= Min[Abs[Differences@#]] & /@ Partition[Join[{Max@#}, Sort@#, {Min@#}], 3, 1] &;

Example use - 1000 reals over (0,1000), get result, create a distribution usable with MMA probability functions:

myList = RandomReal[1000, 1000];

result = newF@myList;

dist = EmpiricalDistribution[result];

Probability[distance < 1, distance \[Distributed] dist]
Mean[dist]

Plot[CDF[dist, x], {x, Min@result, Max@result}, PlotRange -> All]

0.847

0.512673

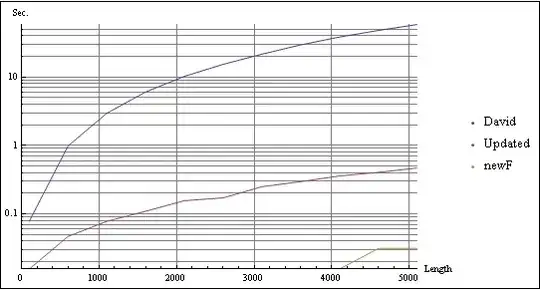
Lastly, if dealing with really large lists, this less pretty code will get you 2X+ advantage over newF using some trickery to better vectorize things:

newF3 = With[{s = Sort@#},
    Flatten[{Abs[Subtract @@ s[[;; 2]]], 
      With[{a = Abs[Differences[Transpose@Partition[s, 3, 1]]]},
       Divide[Subtract[Total@a, Abs[Subtract @@ a]], 2]]
      , Abs[Subtract @@ s[[-2 ;;]]]}]] &;

If you happen to be dealing with integers vs reals, change the Divide[...,2] to BitShiftRight[...,1] for a nice bump in speed.

Answer 2

myList = RandomReal[{0, 10}, 1000];

nearestDistanceList = 
EuclideanDistance[Nearest[Complement[myList, {#}], #], #] & /@ myList;

Histogram[nearestDistanceList]