1

In work that I am doing, I am trying to plot multiple zero-counting functions, depending on how a parameter works. For example, if the zeros of one function are {1, 2, 3, 4, 5, 6, 7}, the zeros of another function are {3, 5, 8, 12}, and the zeros of the third function are {7, 10}, my data looks like

SampleDats = {{1, 2, 3, 4, 5, 6, 7}, {3, 5, 8, 12}, {7, 10}};

For the counting function, the Count documentation gives an answer akin to 

CountingFcn[dat_, r_] := Count[dat, u_ /; u < r];

which can be used on each row of the table in turn.

Of course, if I just write a Table, the HoldAll masks the differences between the list elements, and we get 

PlotCountsBasic[dat_, {rMin_, rMax_}] := 
Plot[Table[CountingFcn[dat[[j, All]], r], {j, 1, Length[dat]}], {r, 
rMin, rMax}, ImageSize -> Large] ;
PlotCountsBasic[SampleDats, {0, 13}]

which yields 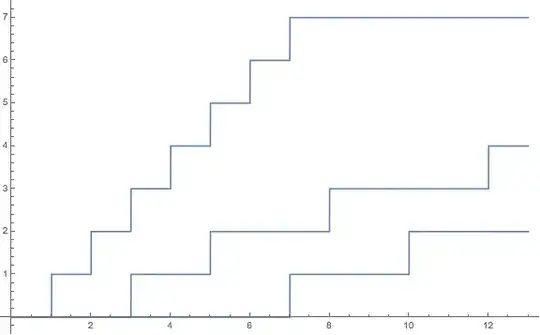Evaluated in wrong order --- all blue

So far, of course nothing is outside the scope of Question 1731.

The trouble is that when I do set Evaluated -> True, I get the zero-function.

PlotCountsEval[dat_, {rMin_, rMax_}] := 
Plot[Table[CountingFcn[dat[[j, All]], r], {j, 1, Length[dat]}], {r, 
  rMin, rMax}, ImageSize -> Large, Evaluated -> True] ;
PlotCountsEval[SampleDats, {0, 13}]

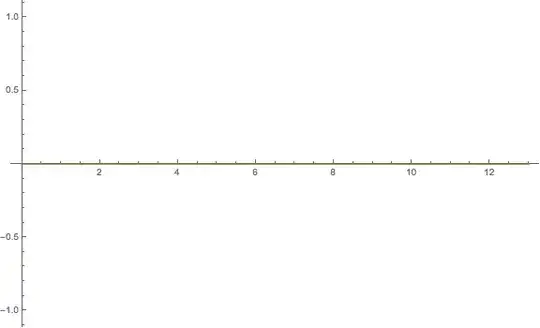
Zero-function plots!

This is not really an issue with Plot, but Evaluate is evaluating "too quickly" for the counting command to give any real value. Compare:

Evaluate[Table[
CountingFcn[SampleDats[[j, All]], 7], {j, 1, Length[SampleDats]}]]
(*{6, 2, 0}*)
Clear[r];
Evaluate[Table[
CountingFcn[SampleDats[[j, All]], r], {j, 1, Length[SampleDats]}]]
(*{0, 0, 0}*)

Question: Given that the Evaluate trick won't work for the counting function as written, what is the best way around? Is the right way to revise the counting-function, or is the right way to use more esoteric commands in the Plot?

Configuration: Mac OS X Yosemite (department computer), Mathematica 10.0.2.0.

Community
  • 1
user52733
  • 145
  • 8

2 Answers2

5

I might be missing the point of the question but I think you just need _?NumericQ:

ClearAll[CountingFcn]

CountingFcn[dat_, r_?NumericQ] := Count[dat, u_ /; u < r];

This prevents the evaluation of the function until r is numeric. Now:

PlotCountsEval[SampleDats, {0, 13}]

enter image description here

Reference: PatternTest, NumericQ

Mr.Wizard
  • 271,378
  • 34
  • 587
  • 1,371
5

Plot is not really for discrete results like this, though one can harangue it into doing so. Better to use DiscretePlot or ListPlot, e.g.:

Table[CountingFcn[SampleDats[[j, All]], r], {j, 1, Length[SampleDats]}, {r, 0, 13}];

ListPlot[%, Joined -> True, InterpolationOrder -> 0,

DataRange -> {0, 13}]

enter image description here

ciao
  • 25,774
  • 2
  • 58
  • 139
  • I can't tell if this was just a convenient example for the OP; I'll hold my vote until I see what he says. – Mr.Wizard Apr 22 '15 at 05:44
  • @Mr.Wizard: Yes, not completely clear from OP what's desired, so I punted... – ciao Apr 22 '15 at 05:45
  • It's a point. However, @Mr.Wizard is correct in that I oversimplified a bit; if n(r) is the counting function, I "really" want to plot n(r)/Sqrt[r], to see this appears to approach a constant. [I know for my functions that n(r)/Sqrt[r] is asymptotically bounded above, but not obviously asymptotically bounded below by any nonzero bound.] The zeros of my actual functions are just some real numbers. Of course, they are spaced out enough so that a Listplot would work, but I'm not yet convinced that such is the "right" way around. – user52733 Apr 22 '15 at 05:53
  • Still, @rasher, your answer is a good workaround, so +1. – user52733 Apr 22 '15 at 05:58