Finding roots of transcendental equation and collecting into a list

Question

I am working on a physics reserach project for school and I have run into some troubles working Mathematica. I am a fairly inexperienced mathematica user so any help would very much be appreciated.

I need to find the roots of the transcendental equation $$\zeta_n \tan(\zeta) - \sqrt{R^2-\zeta^2_n}=0$$ and then collect them into a list, $\{\zeta_n\}$, which I can sum over.

FindRoot works but only finds one root at a time. For example $R^2=18$ gives

FindRoot[Sqrt[18. - zeta^2] - zeta Tan[zeta] == 0, {zeta, 3}]

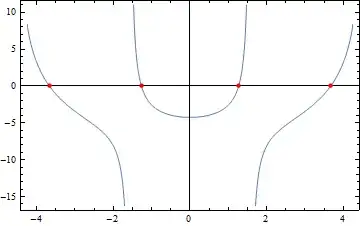
{zeta -> 3.66808} From a plot of the function I know there should be two roots for this particular value of $R$, however FindRoot only gives one.

I have had no luck with NSolve or Solve either.

NSolve[xi[zeta, Erg4]- zeta*Tan[zeta] == 0, zeta]

NSolve[Sqrt[18. - zeta^2] - zeta Tan[zeta] == 0, zeta]

Also once I have succeeded in finding all roots how does one put them in an indexed set ${\zeta_n}$.

score 5 · Answer 1 · answered Apr 23 '15 at 01:22

With[{maxR = 10},
 Manipulate[
  expr = Sqrt[R^2 - zeta^2] - zeta Tan[zeta];
  zero = zeta /. NSolve[{expr == 0,
       R^2 - zeta^2 >= 0}, zeta] // Quiet;
  Column[{
    Plot[expr, {zeta, -maxR, maxR},
     Exclusions -> {Cos[zeta] == 0},
     PlotRange -> {{-maxR, maxR}, {-25, 40}},
     Epilog -> {Red, AbsolutePointSize[4],
       Point[{#, 0} & /@ zero]},
     AspectRatio -> 1],
    zero},
   Alignment -> Center],
  {{R, Sqrt[18]}, 0, maxR, Appearance -> "Labeled"}]]

enter image description here

score 2 · Answer 2 · answered Apr 23 '15 at 05:20

If the goal is only to obtain the sum of positive roots, then

f[r_] := Total[ζ /. NSolve[{Sqrt[r^2 - ζ^2] - ζ Tan[ζ] == 0, 
           r^2 - ζ^2 >= 0, ζ > 0}, ζ]]

produces this quantity. For instance,

Plot[f[r], {r, .1, 10}, AxesLabel -> {R, Total}]

Mathematica graphics

Quiet is used only to suppress the occasional information message,

Solve::ratnz: Solve was unable to solve the system with inexact coefficients. The answer was obtained by solving a corresponding exact system and numericizing the result. >>

score 2 · Answer 3 · answered Apr 23 '15 at 14:23

I'm going to guess that you're trying to solve for the even states of the finite square well in quantum mechanics. Note that the number of roots is just determined by $R$, and is Floor[R/π]; plot the graphs of $\zeta \tan \zeta$ and $\sqrt{R^2 - \zeta^2}$ to see why this is so. Moreover, it's not too hard from this graph to see that the first root will always be in the region $[0, \pi/2)$; the second root will be in the range $[\pi, 3\pi/2)$; the third will be in the range $[2\pi, 5\pi/2)$; and so forth.

FindRoot allows for an option where you can provide it with values $\{ x, x_{start}, x_{min}, x_{max}\}$, which will search for a root within the interval $[x_{min}, x_{max}]$. Since we know where the roots are for this function, we can take advantage of this functionality like so:

nroots[R_] := Floor[R/\[Pi]] + 1;
roots[R_] := Table[FindRoot[Sqrt[R^2 - ζ^2] - ζ Tan[ζ] == 0,
 {ζ, n π + π/4, n π, n π + π/2}], {n, 0, nroots[R] - 1}]

nroots[3√2]
(* {{ζ -> 1.26743}, {ζ -> 3.66808}} *)

The analogous problem for the odd-parity states is left as an exercise for the student. :-)

Thank you for your answer it was very helpful. I am using your method as it was the easiest to understand. However, in some cases Mathematica thinks there is a root which lies just outside the range given to FindRoot and mathematica includes it inside the table. Is there an easy way to tell Mathematica that I don't want it to do this? — APok, Apr 25 '15 at 05:38
@APok: Sorry for the delayed reply. I haven't been able to reproduce this problem; can you give me a value of R for which this happens? — Michael Seifert, Apr 28 '15 at 16:38

score 2 · Answer 4 · edited Apr 13 '17 at 12:55

After a slight rearrangement, your equation is a good candidate for the Chebyshev approach, as detailed here and here:

r = Sqrt[18]; f = Sqrt[r^2 - #^2] Cos[#] - # Sin[#] &;
n = 32;
cnodes = Rescale[N[Cos[Pi Range[0, n]/n], 20], {-1, 1}, {-r, r}];
cc = Sqrt[2/n] FourierDCT[f /@ cnodes, 1];
cc[[{1, -1}]] /= 2;

colleague = SparseArray[{{i_, j_} /; i + 1 == j :> 1/2,
                         {i_, j_} /; i == j + 1 :> 1/(2 - Boole[j == 1])},
                        {n, n}] -
            SparseArray[{{i_, n} :> cc[[i]]/(2 cc[[n + 1]])}, {n, n}];

rts = Sort[Select[DeleteCases[
           Rescale[Eigenvalues[colleague], {-1, 1}, {-r, r}],
                   _Complex | _DirectedInfinity], Abs[#] <= r &]];

Plot[x Tan[x] - Sqrt[r^2 - x^2], {x, -r, r},
     Epilog -> {Directive[Red, PointSize[Medium]], 
                Point[Transpose[PadRight[{rts}, {2, Automatic}]]]},
     Exclusions -> {Cos[x] == 0}]

there's the roots!

score 1 · Answer 5 · answered Aug 21 '15 at 17:58

If you only want real solutions, then NSolve will find them if we help it by including the domain for zeta.

R = Sqrt[18];
sol = NSolve[Sqrt[R^2 - zeta^2] - zeta Tan[zeta] == 0 && -R <= zeta <= R]
(*
  {{zeta -> -3.66808}, {zeta -> -1.26743},
   {zeta -> 1.26743},  {zeta -> 3.66808}}
*)

You can save them in an indexed list like this:

roots = zeta /. sol
(*  {-3.66808, -1.26743, 1.26743, 3.66808}  *)

Finding roots of transcendental equation and collecting into a list

5 Answers5

Linked