0

I have a function g=f(x,t). The function "g" came from a numerical integration:

g[x_?NumericQ,t_?NumericQ]:=NIntegrate[tt[x,r,t],{r,rmin,rmax}]

and tt(x,r,t) came from a data file.

How to plot the second derivative of g(x,t) with respect to "t" for a fixed "x" using the ND command?

enter image description here

For the first derivative, I can use:

ListPlot[Table[{y, ND[g[y, t], t, 15]}, {y, 50, 200, 3}]]

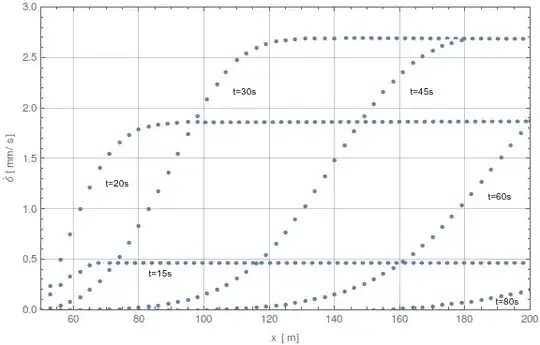
enter image description here

What about the second derivative? The query "numerical partial derivative" have no answer for the second derivative with respect to the same variable.

Community
  • 1
Luis Fernando Moura
  • 137
  • 11
  • It's been awhile since I took calculus... but I'm pretty sure you can take the derivative with respect to t before you integrate with respect to r, as long as rmin, and rmax don't depend on t, (Leibniz rule?). Then I'd do NIntegrate[D[tt[x,r,t],{t,2}], {r,rmin,rmax}]. – N.J.Evans Apr 23 '15 at 01:05
  • @N.J.Evans, in fact it is only an example. My function is more complex than the example. – Luis Fernando Moura Apr 23 '15 at 15:23
  • 1
    You can specify the order of the derivative in the ND function with ND[f[x,y], {x, order}, x0]. – N.J.Evans Apr 23 '15 at 17:34

0 Answers0