8

For a physics application I am considering the radial Bogoliubov-de Gennes equations in two dimensions. In dimensionless form they read as follows $$ \begin{cases} \bigg[\frac{1/4-m^2}{r^2}+2(E-1)\bigg] u_m(r)-2v_m(r)+u_m''(r)=0 \newline \bigg[\frac{1/4-m^2}{r^2}-2(E+1)\bigg] v_m(r)-2u_m(r)+v_m''(r)=0, \end{cases} $$ where $m = 0,1,2$ and $E$ is the energy, a continuous parameter. In fact, one can show that $$ \begin{cases} u_m(r) = -\frac{2\sqrt{r}J_m(kr)}{2+k^2-2E} \newline v_m(r) = \sqrt{r}J_m(kr) \end{cases} $$ is a solution for $k = \sqrt{2(\sqrt{1+E^2}-1)}$ by explicitly substituting it in the equations.

At some point I want to multiply the off-diagonal terms in the system of equations by a function of the radius $r$. This will not be exactly solvable. Hence, I would like to understand how to numerically solve these equations in Mathematica before I make the equations more difficult.

The code I have up to now, is the following:

BdGplot[E1_, Bc1_, m1_] :=
  Module[{E = E1, Bc = Bc1, m = m1}, {btc = 50,

  k = Sqrt[2]*Sqrt[-1 + Sqrt[1 + E^2]],
  uw = -(2 /(2 + k^2 - 2E)),
  ub[r_] := (2/Pi)^(1/2)*uw*Cos[k*r - m*Pi/2 - Pi/4],
  vb[r_] := (2/Pi)^(1/2)*Cos[k*r - m*Pi/2 - Pi/4],

  s = NDSolve[{((1/4 - m^2)/r^2 + 2 (-1 + E)) u[r] - 
    2 v[r] + u''[r] == 0, -2 u[r] + ((1/4 - m^2)/r^2 - 2(1 + E)) v[r] + v''[r] == 0, u[Bc] == ub[Bc], u'[Bc] == ub'[Bc], v[Bc] == vb[Bc], v'[Bc] == vb'[Bc]}, {u,v}, {r, 1/1000, btc}]};

 Plot[Evaluate[{u[r]/(uw*Sqrt[r]), v[r]/Sqrt[r], 
 BesselJ[m, k*r]} /. s], {r, 0.001, btc}, 
 PlotRange -> {{0, btc}, {-2, 2}}, PlotStyle -> {Red, Blue, Orange}]
 ]

The idea is to give boundary conditions at large distance $r$ which are the asymptotic values of the m-th Bessel functions (in the more difficult case, the boundary conditions will be similar). Subsequently I let Mathematica numerically integrate the equations to a small radius $r=0.001$, such that it does not run into trouble at $r=0$.

However, plotting with a command like plotAlpha1 = Manipulate[BdGplot[1.5, Bc, 0], {Bc, 1, 50, 1/10}], one sees that the numerical solutions only match to the exact solution in a certain region. At some point the solutions diverge heavily. Does anybody have any idea how I can resolve this issue?

J. M.'s missing motivation
  • 124,525
  • 11
  • 401
  • 574
Funzies
  • 391
  • 1
  • 13
  • Could you rework your code a bit such that it can be copy&pasted? – user21 Apr 23 '15 at 16:12
  • @user21 I have updated the code, it should be copy-pastable now. – Funzies Apr 24 '15 at 08:00
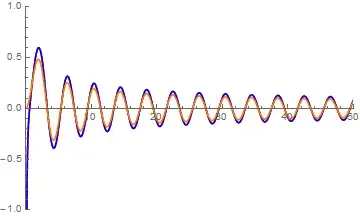
  • I think it might be just numeric precision loss. Try something like WorkingPrecision -> 50 which will improve the situation a lot. You will have to take care that all constants will be given as exact numbers, but that would only mean to change 1.5 to 3/2 for the value in the Manipulate... – Albert Retey Jun 05 '15 at 09:37
  • I think WorkingPrecision->30 should be good enough, and I forgot to mention that this is of course to be used as an option to NDSolve... – Albert Retey Jun 05 '15 at 09:52
  • @AlbertRetey Very surprising! In this case changing 1.5 to 3/2 is necessary, or WorkingPrecision -> 32 won't work at all! I used to think that though the warning NDSolve::precw will be generated, as long as a higher WorkingPrecision is set, approximate numbers in the differential equation won't influence the result. (Actually I never saw this principle failed before!) – xzczd Jun 05 '15 at 13:36
  • 1
    @xzczd : I'm not sure why you did see other behaviour before, but that is the usual rule: precision will never automatically increase, so if you start out with machine precision numbers only in very limited cases increasing WorkingPrecision higher than MachinePrecision will have any effect, and usually not the desired one (AFAIK). To be on the safe side I do use completely "exact" input if I play around with the precision stuff beyond machine precision and that so far has been free from any surprises... – Albert Retey Jun 05 '15 at 15:46

1 Answers1

13

As indicated in the comments, a larger WorkingPrecision (and, when necessary, also a larger MaxSteps) greatly improves the results of BdGplot as defined in the Question. For instance, with WorkingPrecision -> 50, MaxSteps -> 20000

BdGplot[2, 20, 2]

yields

enter image description here

However, the code can be modified to still further improve the accuracy of the result:

BdGplot1[e_,  m_] := Module[
  {btc = 50, r0 = 1/1000, k = Sqrt[2]*Sqrt[-1 + Sqrt[1 + e^2]]},
  uw = -2 /(2 + k^2 - 2 e);
  s = Quiet@NDSolve[{((1/4 - m^2)/r^2 + 2 (e - 1)) u[r] - 2 v[r] + u''[r] == 0,
                     ((1/4 - m^2)/r^2 - 2 (e + 1)) v[r] - 2 u[r] + v''[r] == 0,
                     r0 u'[r0] == (m + 1/2) u[r0], r0 v'[r0] == (m + 1/2) v[r0], 
                     u[r0] == uw Sqrt[r0] BesselJ[m, k*r0], u[btc] == uw v[btc]}, 
                     {u, v}, {r, r0, btc}, WorkingPrecision -> 40, MaxSteps -> 20000];
  Plot[Evaluate[{u[r]/(uw*Sqrt[r]), v[r]/Sqrt[r],  BesselJ[m, k*r]} /. s], {r, r0, btc}, 
      PlotRange -> {{0, btc}, {-1, 1}}, PlotStyle -> {Red, Blue, Orange}]]

BdGplot1[2, 2]

enter image description here

although the modified code is a bit slower, and NDSolve complains about the boundary conditions before producing the correct answer. (The three curves, which appear as one in the plot, agree to six significant figures.)

BdGplot1 readily generalizes to the modified calculation mentioned in the question. The boundary conditions r0 u'[r0] == (m + 1/2) u[r0], r0 v'[r0] == (m + 1/2) v[r0] should be unchanged, the boundary condition u[r0] == uw Sqrt[r0] BesselJ[m, k*r0] is arbitrary and was chosen merely for normalization, and the boundary condition u[btc] == uw v[btc] changes insofar as uw may need to be modified, if the asymptotic ratio of u and v changes.

Addendum

The added option, 

Method -> {"Shooting", "StartingInitialConditions" -> {r0  u'[r0] == (m + 1/2) u[r0], 
    r0 v'[r0] == (m + 1/2) v[r0], u[r0] == uw v[r0], v[r0] == Sqrt[r0] BesselJ[m, k*r0]}, 
    Method -> {"StiffnessSwitching"}}

increases the speed of BdGplot1[2, 20, 2] by a factor of about three.

bbgodfrey
  • 61,439
  • 17
  • 89
  • 156
  • Great, detailed answer, thanks! One question: I tried changing the boundary condition from 50 to 100. In this case, the solutions start to diverge around r = 60, even if I increase the maximum step size and accuracy. Do you have any clue what I should change in this case? – Funzies Jun 08 '15 at 08:33
  • Additionally, for higher energies (from about E = 5) there are some problems as well.. Do you know of any solutions to this? Or perhaps I am just asking too much of Mathematica. – Funzies Jun 08 '15 at 08:41
  • Your equations support two solutions, one with the k in the Question, and the other with k = Sqrt[2]*Sqrt[-1 + I*Sqrt[1 + e^2]], The second solution has the character of a Modified Bessel Function for large e, which grows exponentially. For larger e larger values of WorkingPrecision are needed to prevent the second solution from polluting the first. So, for e == 8, WorkingPrecision -> 80 is needed. Also, be sure to include the Method option that I gave in the Addendum. At some point, just increasing WorkingPrecision is not practical, and I have some other ideas. – bbgodfrey Jun 08 '15 at 13:55
  • @Funzies You state in your question that you want to multiply the off-diagonal terms by a function of the radius r. Is your goal to obtain numerical expressions for u and v, or obtain some averaged quantity, like the phase shift at large r? Also, do your off-diagonal multipliers differ significantly from 1 over a large range of r, or are they highly localized? I have obtained a solution for the multiplier (1 + 5 Exp[-(r - btc/2)^2]), which is fairly localized. The calculation requires a high WorkingPrecision and, therefore, is slow but produces accurate results. – bbgodfrey Jun 09 '15 at 00:11
  • I need to calculate the numerical expressions for u and v for different values of m and E. I'm afraid that the off-diagonal function is horrendous: it is $\exp(i \pm \theta(r))$ for the upper (lower) diagonal, with $\theta(r) = c_0 \log(r)$, where $c_0$ is a negative constant. (It has this weird form because in these type of physics problems the derivative of theta is proportional to the superfluid velocity, which in this case is giving by 1/r). So the function is highly non-localized. However, intuitively I still expect the ordinary BdG results to hold at large r. – Funzies Jun 09 '15 at 07:31
  • @Funzies What is \pm and what is a typical value for c0? – bbgodfrey Jun 09 '15 at 12:40
  • By \pm I just mean that the term on the right diagonal has a plus sign in the exponential and the term on the left diagonal a minus sign. The value of c_0 varies from 0 (homogeneous case, which you solved in your answer) to, say, -3. – Funzies Jun 09 '15 at 14:39
  • @Funzies In other words, the multipliers are r^(I c0) and its conjugate? This changes the character of the asymptotic solution, and I am not certain how to obtain the new asymptotic solution. – bbgodfrey Jun 09 '15 at 18:33