Problem with 3D surface disconnections

Question

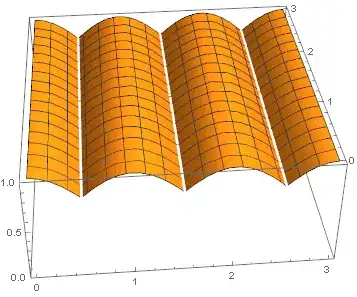
I have a problem with a 3D surface in Mathematica 10.1. The problem is that the surface comes out disconnected even if it shouldn't. Here's a minimal toy example showing the problem:

Plot3D[E^-(x - Round[x])^2, {x, 0, 3}, {y, 0, 3}, PlotRange -> {0, 1}]

the result is

The surface profile (in 2D) is that of a continuous line (even if it is not differentiable at all points):

Plot[E^-(x - Round[x])^2, {x, 0, 3}, PlotRange -> {0, 1}]

2D Profile is connected

Increasing the PlotPoints actually reduce the gaps' width, but doesn't eliminate them.

I have also tried the above code in Mathematica 9 and there's the same problem.

That effect is very awful in the rendering of a much more complex surface intended to reproduce a seashell (with bumps and nodules). Is there any simple workaround to smooth out (not differentiable) surfaces?

Try a combination of Exclusions -> None and a larger number for MaxRecursions. — Virgil, May 04 '15 at 13:52
@Virgil Thanks. I didn't know about the Exclusions -> None option. It seems to work. — Luca M, May 04 '15 at 14:19
related Q/As: White Lines in Contour Plot and 3D Plot, Why does Plot3D omit parts of the surface at kinks? — kglr, May 05 '15 at 15:56
Luca, I hope someday you can post pictures of your simulated seashells. :) — J. M.'s missing motivation, May 06 '15 at 05:31

score 4 · Accepted Answer · answered May 05 '15 at 15:38

4

For the record, this can be solved by setting Exclusions -> None in Plot3D, which tells Mathematica not to exclude subregions of the domain that are associated with discontinuities. Generally, if you want that plot to look sharp, you will have to couple it with a largish number for MaxRecursions:

Plot3D[E^-(x - Round[x])^2, {x, 0, 3}, {y, 0, 3}, 
 Exclusions -> None,
 MaxRecursion -> 10
 PlotRange -> {0, 1}]

plot

answered May 05 '15 at 15:38

Virgil

3,437
16
27

2

Yet another (sneaky!) way to thwart automatic exclusion is to make the definition f[x_?NumericQ] := E^-(x - Round[x])^2 and use that for the plots. – J. M.'s missing motivation May 06 '15 at 04:26
Instead of Exclusions-> None, there should be a command.. Inclusions-> All :) – Narasimham May 06 '15 at 07:02

Problem with 3D surface disconnections

1 Answers1