Switch from logarithmic to linear scaling partway along a plot's axis

Question

In the 2015 Planck satellite results, they give the latest plot of the temperature power spectrum of the cosmic microwave background, which I show below. (I am only interested in the main plot; you can ignore the residuals at the bottom.)

Notice that there is a dotted vertical line at $\ell=30$, and the x-axis to the right of that line is linear while to the left it is logarithmic.

How close of an approximation to this effect can I create in Mathematica?

Answer 1

Ok, here's a very brief toy example while I don't have access to my desktop computer at work.

It's easy enough to figure out, that a LogPlot of f is basically the plot of Log[f[x]]. And A LogLinearPlot is the plot of f[Exp[x]]. But we can extend this to arbitrary scalings of the axes.

I start with defining a piecewise function which maps x values between 0 and 1 to the interval from 1 to 10 logarithmically and x values between 1 and 2 to the interval 10 to 100 linearly, as well as the inverse of that.

g[x_] := Piecewise[{{10^x, 0 <= x < 1},
                    {Rescale[x, {1, 2}, {10, 100}], x >= 1}}]
inverseg[x_] := 
 Piecewise[{{Log[10, x], 1 <= x < 10},
            {Rescale[x, {10, 100}, {1, 2}], x >= 10}}]

Then if you have the CustomTicks package:

Needs["CustomTicks`"];
ticks = LinTicks[1, 10, TickPostTransformation -> inverseg]~Join~
   LinTicks[10, 100, TickPostTransformation -> inverseg];

If you don't have it:

ticks = {N@inverseg@#, 
     ToString@#, {0.01, 0}, {}} & /@ (Range[2, 10, 2]~Join~
     Range[20, 100, 20]);

Finally (I show Sin[x] in this toy example):

Plot[Sin[g[x]], {x, 0, 2}, Ticks -> {ticks, Automatic}]

Note, how according to the x-y coordinates taken from the axes labels this is just the regular Sin[x] function, but everything is distorted such, that we see the desired log scaling before 10 and linear scaling after.

This plot was generated without using the CustomTicks package, hence lazy and without minor ticks. I'll go into more details tomorrow.

Update 05.05.15

Writing out these piecewise functions by hand is tedious. I've automated this.

Firstly, a function I called MapLog, though logRescale may have been more appropriate. Although, unlike Rescale[x, {x1, x2}, {y1 y2}] where simply swapping the 2nd and 3rd argument gives you the inverse function, with a logarithmic/exponential mapping it's a bit less straightforward.

MapLog[{x1_, x2_, y1_, y2_}, type_String: "Direct"] :=
    Which[
        type == "Direct", (Log[(x2/x1)^(1/(y2 - y1)), #1/x1] + y1 &),
        type == "Inverse", (x1 (x2/x1)^((#1 - y1)/(y2 - y1)) &)]

The default "Direct" form take the interval {x1, x2} and maps it to the interval {y1, y2} logarithmically.

Plot[MapLog[{1, 10, 0, 1}][x], {x, 1, 10}]

MapLog[{1,10,0,1}, "Inverse"]

will naturally give the inverse of such an operation.

Next comes the main function AxisBreaks, which handles the construction of the direct and inverse transformation functions for the ticks and coordinates.

Options[AxisBreaks] = {Output -> "Direct"};
AxisBreaks[specs :
             PatternSequence[{{_?NumericQ, _?NumericQ, _?NumericQ, _String : "Lin"} ..}],
           opts : OptionsPattern[]] := 
    Module[{
        fullspecs = (If[Length[#] == 3, Join[#, {"Lin"}], #, #] &) /@ specs,
        ranges2 = Accumulate[specs[[All, 3]]],
        ranges1 = Accumulate[specs[[All, 3]]] - specs[[All, 3]],
        expspecs, dirfunc, invfunc, output
        },
    expspecs = 
     Transpose@{fullspecs[[All, 1]], fullspecs[[All, 2]], ranges1, ranges2, fullspecs[[All, 4]]};

    If[OptionValue[Output] == "Direct",
       dirfunc[x_] :=
       Piecewise[Table[
        {Which[j[[5]] == "Lin", Rescale[x, j[[1 ;; 2]], j[[3 ;; 4]]],
               j[[5]] == "Log", MapLog[j[[1 ;; 4]], "Direct"][x]], 
         j[[1]] <= x <= j[[2]]}, {j, expspecs}]];];

    If[OptionValue[Output] == "Inverse",
       invfunc[x_] := 
       Piecewise[Table[
        {Which[j[[5]] == "Lin", Rescale[x, j[[3 ;; 4]], j[[1 ;; 2]]],
               j[[5]] == "Log", MapLog[j[[1 ;; 4]], "Inverse"][x]], 
         j[[3]] <= x <= j[[4]]}, {j, expspecs}]];];

    Which[OptionValue[Output] == "Direct", output = dirfunc;,
          OptionValue[Output] == "Inverse", output = invfunc;];
    output
    ]

Usage is as follows:

specs = {{1, 30, 1, "Log"}, {30, 500, 4}};
dg = AxisBreaks[specs];
ig = AxisBreaks[specs, Output -> "Inverse"];

Which means in plain English "give me a function, that maps the interval {1, 30} logarithmically to 1 part of the plot and the interval {30, 500} to 4 parts of the plot (specifically, to {0, 1} and {1, 5}, respectively. Also give me the inverse function of this."

Then a little helper to generate the ticks:

makeTicks[func_, major_List, minor_List: {}] := 
({func@#, ToString@#, {0.01, 0}, {}} & /@ major) ~Join~ 
({func@#, "", {0.005, 0}, {}} & /@ minor);

Usage:

major = {2, 10, 30}~Join~Range[100, 500, 100]; (* can't be bothered to make minor ticks *)
ticks = makeTicks[dg, major];

Basically give the transformation function as the first argument, the list of major ticks as the second, minor ticks are an optional third argument.

Now plot f[x], replacing as f[ig[x]] (ig is the inverse transformation), and if you want to plot between x1 and x2, you now need to substitute dg[x1] and dg[x2] (dg is the direct transformation).

Plot[Sin[15/Sqrt[ig@x]], {x, dg[1], dg[500]}, 
 Ticks -> {ticks, Automatic}, PlotRange -> Full]

Neat examples

This goes beyond the scope of the OP, but AxisBreaks can do a lot more, that I'd like to showcase.

LogLinearPlot for negative values? Negative and positive values? No problem.

specs = {{-1000, -5, 2, "Log"}, {-5, 5, 1}, {5, 1000, 2, "Log"}};
dg = AxisBreaks[specs];
ig = AxisBreaks[specs, Output -> "Inverse"];
ticks = 
 makeTicks[dg,
  {-1000, -300, -100, -30, -10, 10, 30, 100, 300, 1000}~Join~Range[-4, 4, 2]];
Plot[Log[1 + y^2] /. y -> ig[x], {x, dg[-1000], dg[1000]}, 
 Ticks -> {ticks, Automatic}, AxesOrigin -> {dg[0], 0}]

Generating a broken or snipped axis?

The graphical part aside (that's straighforward with Epilog), how to show two datasets like

data1 = RandomReal[{0, 1}, 30];
data2 = RandomReal[{1000, 1001}, 30];

on one graph? Simple, the intervals need not be continuous, just monotonically increasing and log mapping mustn't cross zero.

specs = {{0, 1.1, 1}, {999.9, 1001.1, 1}};
dg = AxisBreaks[specs];
ig = AxisBreaks[specs, Output -> "Inverse"];
ticks = makeTicks[dg, Range[0, 1, .2]~Join~Range[1000, 1001, .2]];
ListPlot[{dg /@ data1, dg /@ data2}, Ticks -> {Automatic, ticks}, 
 Joined -> True]

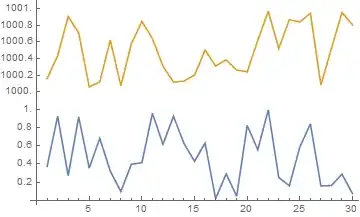
Note, that as it is now the y-axis being rescaled, I apply the direct transformation to the data (dg, not ig), and I actually don't need the inverse. Also I slightly padded the intervals being remapped, as they aren't continuous.

Both axes at the same time. Say we have four datasets which occupy rather different ranges (smallX, smallY), (smallX, bigY), (bigX, bigY), (bigX, smallY), although with some limitations.

data1 = Transpose@{Range[1, 10], 
    Range[.5, 5, .5] + RandomReal[{0, 0.3}, 10]};
data2 = Transpose@{Range[1000, 1100, 10], 
    Range[5, 0, -.5] + RandomReal[{0, 0.3}, 11]};
data3 = Transpose@{Range[1000, 1100, 10], 
    Range[500, 1500, 100] + RandomReal[{0, 10}, 11]};
data4 = Transpose@{Range[1, 10], 
    Range[1500, 600, -100] + RandomReal[{0, 10}, 10]};
specsx = {{0, 11, 1}, {990, 1110, 1}};
specsy = {{0, 6, 1}, {500, 1600, 1}};
dgx = AxisBreaks[specsx];
dgy = AxisBreaks[specsy];
ticksx = makeTicks[dgx, Range[1, 10]~Join~Range[1000, 1100, 20]];
ticksy = makeTicks[dgy, Range[1, 5]~Join~Range[500, 1500, 200]];
ListPlot[Map[{dgx[#[[1]]], dgy[#[[2]]]} &, {data1, data2, data3, 
   data4}, {2}], Ticks -> {ticksx, ticksy}]

In the case of ListPlot where data are given as x-y pairs, we apply the direct transform to the x coordinate too. The inverse is again not needed.

Feel free to suggest further examples.

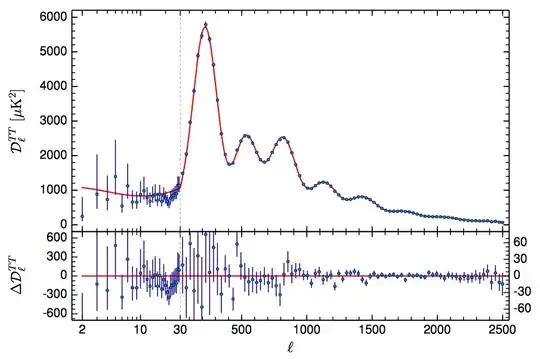
Bonus - reproduction of the graph in OP

Simply load the definitions of AxisBreaks and MapLog and run below code to get

specs = {{2, 30, 2, "Log"}, {30, 2500, 4}};
dg = AxisBreaks[specs, Output -> "Direct"];
ig = AxisBreaks[specs, Output -> "Inverse"];
makeTicks[func_, major_List, 
   minor_List: {}] := ({func@#, ToString@#, {0.02, 0}, {}} & /@ 
     major)~Join~({func@#, "", {0.01, 0}, {}} & /@ minor);
major = {2, 10, 30}~Join~Range[500, 2500, 500];
minor = Range[3, 9]~Join~{20}~Join~Range[100, 2400, 100];
ticks = makeTicks[dg, major, minor];
func[x_] := 
 Total@Thread[((#2 #3 x^2)/(#3^2 x^2 + (-x^2 + #1^2)^2) &)
     [{2, 250, 600, 800, 1500}, {2, 100, 40, 40, 40}, {30, 200, 200, 200, 1000}]]
 Plot[10^4 func[ig[x]], {x, dg[2], dg[2500]}, FrameStyle -> Thick, 
 ImageSize -> 600, BaseStyle -> 16, Frame -> True, 
 FrameTicks -> {ticks, Automatic}, 
 Epilog -> {Gray, Dashed, Line[{{dg[30], -200}, {dg[30], 5500}}]}]

Answer 2

If you are comfortable using undocumented and unsupported functionality we can do this with a ScalingFunctions option as I did for ListLogLinearPlot for the whole real numbers.

(* listability *)
(self :    fn[off_, scale_])[x_List] := self /@ x
(self : invfn[off_, scale_])[x_List] := self /@ x

fn[off_, scale_][x_?NumericQ] :=
  If[x < off, Log[x], x/scale + (Log[off] - off/scale)]

invfn[off_, scale_][x_?NumericQ] := 
  If[x < Log[off], Exp[x], off + x scale - scale Log[off]]

splitlog[n_, scale_: 10] := {fn[n, scale], invfn[n, scale]}

To use it:

Plot[Sin[15/x], {x, 1, 50},
 PlotRange -> All,
 ScalingFunctions -> {splitlog[9], None},
 GridLines -> {{9}}
]

The first parameter is the x point at which to switch from log to linear. The second (optional) parameter of splitlog controls relative scale of the two halves of the plot:

Table[
  Plot[Sin[15/x], {x, 1, 50},
    PlotRange -> All,
    ScalingFunctions -> {splitlog[point, scale], None},
    GridLines -> {{point}},
    ImageSize -> 180
  ],
  {point, {3, 15, 35}},
  {scale, {2, 10, 30}}
] // GraphicsGrid