so what I want to do is take an undirected graph, and remove all the "dead ends" (that is, vertices that are attached to only one other vertex), but do it in such a way that it does it until reaches "steady state", i.e., it keeps doing this until there are no more dead ends to remove.
For example, here's a starting graph, h:

I would like it to remove vertices 4 and 5 (and edges 3<->4 and 4<->5, of course), just leaving the loop really.
So I made a really simple function:
RemoveDeadEnds[g_] := (
gcopy = g;
Do[
If[EdgeCount[gcopy, i <-> _] == 1, gcopy = VertexDelete[gcopy, i]];
, {i, Length@VertexList@g}];
Return@gcopy;
)
The problem is that, in the case of the example I had above, it just remove Vertex 5, because at the time in the loop when it checks vertex 4, vertex 4 had 2 edges. By the time it removes vertex 5, when vertex 4 has 1 edge (and should thus be removed), it is already past it, so it returns:
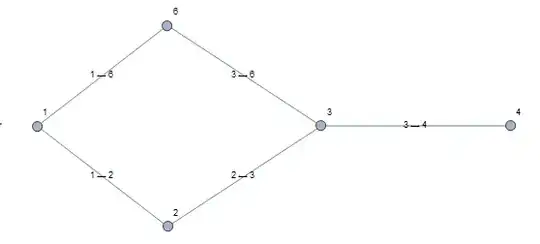
Obviously I could loop it several times. But that's obviously inelegant, and who knows how long this chain of dead ends is?
I can think of another way, but a little messy: you have a nested function so when you remove a vertex, you check the other vertex it was (formerly) attached to, and test that one. But that's not ideal either.
Is there a better way to do it? Ideally some magical Mathematica function that's already built in?
Edit: I implemented the method I said right above, using recursion:
CheckAndRemoveDeadEnd[g_, node0_] := (
gcopy = g;
If[EdgeCount[gcopy, node0 <-> _] == 1,
j = First@AdjacencyList[gcopy, node0];
gcopy = VertexDelete[gcopy, node0];
gcopy = CheckAndRemoveDeadEnd[gcopy, j];
];
Return@gcopy;
)
DeleteAllDeadEnds[g_] := (
gcopy = g;
Do[
gcopy = CheckAndRemoveDeadEnd[gcopy, i];
, {i, Max@VertexList@g}];
Return@gcopy;
)

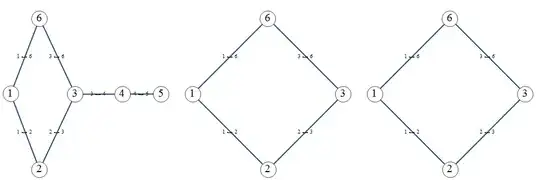
ReplaceRepeated... (or//.in shorthand). – LLlAMnYP May 06 '15 at 20:40