This graph–also known as a Lissajous figure–contains so many self-intersections.How can I highlight them?
ParametricPlot[{Sin[100 t], Sin[99 t]}, {t, 0, 2 π},
PlotRange -> All]
This graph–also known as a Lissajous figure–contains so many self-intersections.How can I highlight them?
ParametricPlot[{Sin[100 t], Sin[99 t]}, {t, 0, 2 π},
PlotRange -> All]
I will start with the most general Lissajous figure, which has a parametric equation as follows:
$$ x(t) = f_a(at+\phi_a) \\ y(t) = f_b(bt+\phi_b) \\ t \in [0,2\pi) $$
Where:
$$ f_a, f_b \in \{\sin, \cos\} \\ a, b \in \mathbb{N} \\ \phi_a, \phi_b \in [0, 2\pi) $$
Note that this curve is periodic, so we can "shift" the range of $t$ without changing the curve. Consider one such shift, given by $t \to t'-\frac{\phi_b}{b}$. This gives the new parameterization:
$$ x(t') = f_a\left(a\left(t'-\frac{\phi_b}{b}\right)+\phi_a\right) =f_a\left(at'+\left(\phi_a-\frac{a}{b}\phi_b\right)\right) \\ y(t') = f_b\left(b\left(t'-\frac{\phi_b}{b}\right)+\phi_b\right) = f_b(bt') \\ t \in [0,2\pi) $$
This shows that we can eliminate one of the phase parameters and still describe the entire set of Lissajous figures. At this point we can also notice that $\sin$ and $\cos$ are related by a phase shift of $\pi/2$, so we can absorb the choice of function into the phase parameter, giving us the simplified equation:
$$ x(t) = \cos(at+\phi) \\ y(t) = \cos(bt) \\ t \in [0,2\pi) $$
Finally, take $d=\gcd(a,b)$. This means there exist integers $a'$ and $b'$ such that $a=a'd$ and $b=b'd$, so that:
$$ x(t) = \cos(a'(dt)+\phi) \\ y(t) = \cos(b'(dt)) \\ $$
This is the same curve as the one described by $a'$ and $b'$, except covered $d$ times. Therefore we can describe the entire set of Lissajous figures if we restrict ourselves to cases where $a$ and $b$ are coprime, i.e. $\gcd(a,b)=1$.
Now consider a self-crossing of the Lissajous figure. Such a point occurs when two distinct values of $t$ give the same $x,y$ coordinates:
$$ x(t_1)=x(t_2) \to \cos(at_1+\phi) = \cos(at_2+\phi) \\ y(t_1)=y(t_2) \to \cos(bt_1) = \cos(bt_2) $$
The cosine function is periodic, so one way for two cosines to be equal is for their arguments to differ by a factor of $2\pi$:
$$ \alpha=\beta+2\pi n\to \cos\alpha=\cos\beta $$
However, the cosine function is also even, so it is also possible for one argument to be the negative of the other (plus a factor of $2\pi$):
$$ \alpha=-\beta+2\pi n\to \cos\alpha=\cos\beta $$
Note that at all of the self-crossings, one branch of the curve is moving in an "upwards" diagonal direction and the other is moving in a "downwards" diagonal direction. This means that one of $x$ or $y$ must obey the "negated" equality, so we have one of:
$$ at_1+\phi = at_2+\phi+2\pi n \\ bt_1 = -(bt_2)+2\pi m \\ \textrm{or} \\ at_1+\phi = -(at_2+\phi) + 2\pi n\\ bt_1 = bt_2 + 2\pi m $$
These two systems of equations are linear in $t_1$ and $t_2$ so they each have a unique solution:
$$ t_1 = \left(\frac{n}{a}+\frac{m}{b}\right)\pi - \frac{\phi}{a} \\ t_2 = \left(\frac{n}{a}-\frac{m}{b}\right)\pi - \frac{\phi}{a} \\ \textrm{or} \\ t_1 = \left(\frac{n}{a}+\frac{m}{b}\right)\pi \\ t_2 = \left(-\frac{n}{a}+\frac{m}{b}\right)\pi $$
This gives the following sets of intersection points:
$$ (x,y) = \left(\cos\left(n\pi + \frac{a}{b}m\pi\right), \cos\left(\frac{b}{a}n\pi + m\pi - \frac{b}{a}\phi)\right)\right) \\ 0\le n\le a-1,\quad1 \le m \le b-1\\ \textrm{and} \\ (x,y) = \left(\cos\left(n\pi + \frac{a}{b}m\pi + \phi\right), \cos\left(\frac{b}{a}n\pi + m\pi\right)\right) \\ 1\le n\le a-1,\quad0 \le m \le b-1 $$
Plotting these points in Mathematica:
Manipulate[
ParametricPlot[{Cos[a t + ϕ], Cos[b t]}, {t, 0, 2 Pi},
PlotLabel -> {a, b}, AspectRatio -> Automatic, Axes -> False,
Epilog -> {Red, PointSize[Large],
Table[Point[{Cos[(n + a/b m)Pi], Cos[(b/a n + m)Pi - b/a ϕ]}],
{n, a}, {m, b - 1}],
Table[Point[{Cos[(n + a/b m)Pi + ϕ], Cos[(b/a n + m)Pi]}],
{n, a - 1}, {m, b}]
}
],
{{a, 5}, 2, 20, 1},
{{b, 4}, Select[Range[a], CoprimeQ[a, #] &]},
{{ϕ, Pi/10}, 0, 2 Pi}
]

Count[_, _Point, Infinity] on my table of plots, then pass the counts to Rationalize@Chop@Fit[_, {1, a, b, a b}, {a, b}].)
– 2012rcampion
May 13 '15 at 13:51
One way (whew, there are a lot of intersections! -- here's a shorter version):
sol = NSolve[{Sin[10 t], Sin[9 t]} == ({Sin[10 t], Sin[9 t]} /. t -> s) &&
0 <= t < s < 2 Pi, {t, s}];
ParametricPlot[{Sin[10 t], Sin[9 t]}, {t, 0, 2 π},
Epilog -> {Red, PointSize[Large], Point[{Sin[10 t], Sin[9 t]} /. sol]}]

({Sin[100 t], Sin[99 t]} will take a lot longer.)
General solution via Mathematica that is not too slow
Solve returns solutions in the form ConditionalExpression, and the condition can be used to generate the values {m, n} for each point of intersection (via Solve inside Block).
gensols = Cases[
Solve[(-a t + a s == 2 Pi m || a t + a s == Pi + 2 Pi m) &&
(b t - b s == 2 Pi n || b t + b s == Pi + 2 Pi n) &&
a > b > 0 && {a, b, m, n} ∈ Integers &&
0 <= t < s < 2 Pi, {s, t}],
HoldPattern[t -> t0_] :> {t -> t0}, 2];
Block[{a = 100, b = 99},
pts = Flatten[
Hold[{Sin[a t], Sin[b t]} /. Solve[Last[t], {m, n}]] /. gensols // ReleaseHold,
1]
] // Length // AbsoluteTiming
(* {1.55879, 19601} *)
ParametricPlot[{Sin[100 t], Sin[99 t]}, {t, 0, 2 Pi},
PlotStyle -> {Black, Thickness[0.0015]}, PlotPoints -> 3000,
Epilog -> {GraphicsComplex[N@pts, {Red, PointSize[0.003], Point[Range@Length@pts]}]}]
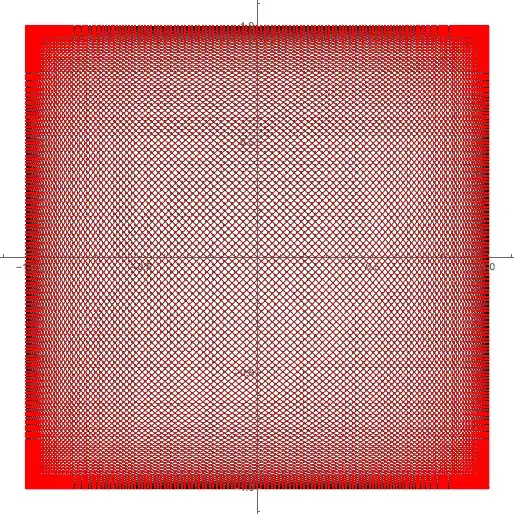
NSolve might be converting the trig. eqns. to polynomial ones -- ouch. The difference between solving (this answer) and having been solved (rcampion2012's) is to be expected. You must be making a pretty big poster to show all those points! :)
– Michael E2
May 11 '15 at 12:31
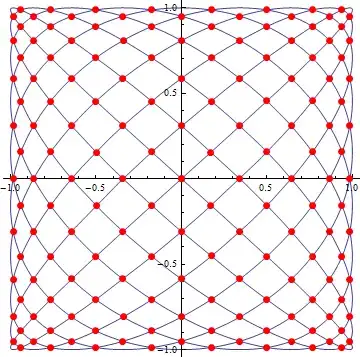
Graphics`Mesh`MeshInit[];
eps = 1/1000000;
pp = ParametricPlot[{Sin[10 t], Sin[9 t]}, {t, eps, 2 π}];
intersections = Graphics`Mesh`FindIntersections[pp];
Show[pp, Epilog -> {Red, PointSize[Large], Point@intersections}]
Graphics`Mesh`FindIntersections[ParametricPlot[{Sin[100 t], Sin[99 t]},
{t, eps, 2 π}]] // Length // Timing
{0.078125, 20330}
Row[Show[plt = ParametricPlot[{Sin[# t], Sin[(# - 1) t]}, {t, 0, 2 π}],
ImageSize -> 300, Epilog -> {Red, PointSize[.2/#],
Point@Graphics`Mesh`FindIntersections[plt]}] & /@ {5, 10, 20, 50}]
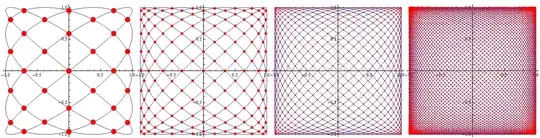
See also: this answer linked in @Guesswhoitis's comment above.
Cases[...] in your comment above and failed to click the link you provided. Yes, it does work; and directly on the graphics input without the extra need to extract the lines.
– kglr
May 11 '15 at 21:58
??*`*Intersections*.
– kglr
May 12 '15 at 11:11
Graphics`Mesh`GeometryPlot ? I don't get any useful infomation from ??
– WateSoyan
May 12 '15 at 15:45
GeometryPlot before. In some cases, you can pass junk as an argument to the function, and if you are lucky, you get an error message that suggests what kind of input is expected. So, trying Graphics`Mesh`GeometryPlot[blah] gives blah was encountered where a Graphics primitive or directive was
expected. So, there you have it: GraphicsMeshGeometryPlot[ Polygon@{{0, 0}, {0, 1}, {1, 0}}, PlotStyle -> Red] works!
– kglr
May 12 '15 at 16:11
Graphics or Plot? Well... perhaps: it has some options that Graphics does not; and, whereas Plot takes a function as the first argument, this one takes a graphics primitive...
– kglr
May 12 '15 at 16:11
I find a workaround which can find all that exact self-intersections:
sol = Solve[(100 (t1 - t2) == 2 k1 \[Or]
100 (t1 + t2) == (2 k1 + 1)) && (99 (t1 - t2) == 2 k2 \[Or]
99 (t1 + t2) == (2 k2 + 1)), {t1, t2}];
Flatten[({t1, t2} /. # /. Solve[(0 <= t1 < t2 < 2) /. #, {k1, k2}, Integers]) & /@ sol, 1]
Flatten[({t1, t2} /. # /. Solve[(0 <= t1 < t2 < 2) /. #, {k1, k2}, Integers]) & /@ sol, 1] to get each solution exactly once. (I was working along similar lines, but I was trying to get the solution even faster.)
– Michael E2
May 11 '15 at 13:52
Cos[Pi Range[2 (n - 1) - 1]/(2 (n - 1))]and y-coordinatesCos[Pi Range[2 (n - 1) + 1]/(2 (n - 1) + 2)]. – 2012rcampion May 11 '15 at 03:34Line[]objects from a plot of the curve (Cases[]is useful here), split any polylines present into simple lines of the formLine[{pt1, pt2}], and then use a line intersection algorithm on the lines produced. Polishing withFindRoot[]is optional. – J. M.'s missing motivation May 11 '15 at 05:02