0

We know about the possibility of series expansion of a function in Mathematica. Same as below, where a function f[a x] is expanded around zero up to 5th order.

Series[f[a x], {x, 0, 5}]=

enter image description here

The function f[a x] can be an Exponential function such as Exp[a x]; and it can be shown with the series:

enter image description here

Are there any way to expand an Exponential function in which a differential operator is contained? same as:

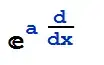
enter image description here

the desired case must be written by the series:

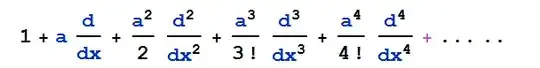
enter image description here

or by clear amounts of factorials:

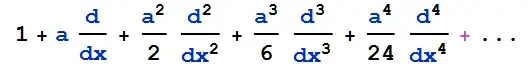
enter image description here

Although we know that for Mathematica it will be meaningless, because in the series must exist the value of the function (f[x]) in the point around which the function has to be expand (I mean f[0] in the above example). But in the differential form there is not this value. But actually, in quantum mechanic, there are many exponential functions with differential operators which must be expanded as a series and we don't know how we can do it!

enzotib
  • 1,094
  • 7
  • 20
Unbelievable
  • 4,847
  • 1
  • 20
  • 46
  • Do you actually need to write out the differential operator, or do you just need a translation operator? It's easy to write a translation operator. For example, T[x_, a_] := Function[expression, expression /. {x -> x - a}]. Then T[x,7]@f[x] evaluates to f[ -7 + x ] while T[x, a]@f[a] becomes f[-a+x] while T[x, a]@f[y] evaluates to f[y]. If you need something that operates on a formal parameter it may be more tricky... – evanb May 16 '15 at 05:42
  • Really it acts as translational operators but as you know may be there is a rotational operator or something else. In general I wanted to know how we can show this procedure. @jens, addresses an answer, I should check it for our purpose. – Unbelievable May 16 '15 at 07:10

0 Answers0