5

My code: 

r5 = 47000;
vcc = 3.3;
hfe = 420; (* BC337-40: 250 *)
vbe = 0.6;
r4 = vbe/2*^-6;
ctr = 1;
r1 = 1000000; r2 = r1;
vrms = 230;
vled = 1.5;
v0[t_] := Max[vcc - r5 ic[t], 0.2]
ic[t_] := Min[hfe ib[t] + 0.000005, vcc/r5]
ib[t_] := idar[t] - ir4[t]
ir4[t_] := Min[idar[t], vbe/r4]
idar[t_] := Abs[iled[t]] ctr
iled[t_] := Max[Sign[vi[t]] (Max[Abs[vi[t]] - vled, 0])/(r1 + r2), 0]
vi[t_] := vrms Sqrt[2]  Sin[2 Pi t/20]
pmains[t_] := vi[t] iled[t]
pvcc[t_] := vcc idar[t] + vcc ic[t]
power[t_] := pmains[t] + pvcc[t]
pvccavg = Integrate[pvcc[t], {t, 0, 20}]/20

MMA gives me this result:

enter image description here

which is my list of nested function calls written as one single function. Why doesn't Integrate work here? Note that it does give me results if I split the [0,20] interval in [0,10] and [10,20].

stevenvh
  • 6,866
  • 5
  • 41
  • 64
  • 4
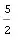
    NIntegrate gives you the answer in less than a second – rm -rf Jul 16 '12 at 16:40
  • @R.M. - Yes, OK, Thanks. But I was wondering why Integrate doesn't work, while it does over the two smaller intervals. Does it have to do with the Abs and/or Max I'm using? – stevenvh Jul 16 '12 at 16:59
  • 1
    Integrate requires 1. Symbolic Input 2. a function that it knows how to symbolically solve. The function that you are integrating using floating point numbers instead of rational numbers. This by itself is a problem since symbolic manipulation of floating point numbers isn't necessarily numerically stable. Additionally, Integrate does not guarantee that it can always find a symbolic solution for an Integral. This is because finding a symbolic solution is often impossible. – Searke Jul 16 '12 at 19:06
  • Although really in this case, the solution is a piecewise function, which is easily solved symbolically. Integrate just doesn't seem to have any functionality for converting the Max/Min statements into a piecewise expression. – Searke Jul 16 '12 at 19:17

3 Answers3

10
Plot[pvcc[t], {t, 0, 20}]

Mathematica graphics

seems to show several discrete regions.

After studying those, this seems to give enough of a hint to accomplish the goal.

In[1]:= Integrate[Simplify[pvcc[t], t > 0], {t, 0, 20}]

Out[1]= 0.00585019
Mr.Wizard
  • 271,378
  • 34
  • 587
  • 1,371
Bill Simpson
  • 484
  • 3
  • 6
4

Or just use Nintegrate[]

pvccavg = NIntegrate[pvcc[t], {t, 0, 20}]

which gives 0.00587397.

M.R.
  • 31,425
  • 8
  • 90
  • 281
3

OK, so NIntegrate seems to be the solution. But I found a possible reason why symbolic integration doesn't work. Take this indefinite integral: 

Integrate[Abs[x], x]

enter image description here

It won't do it. Apparently Abs sees the argument as complex, because 

Integrate[Abs[x], x, Assumptions :> Element[x, Reals]

does work:

enter image description here

It's not a complete explanation though, because if we make the first form into a definite integral 

Integrate[Abs[x], {x, -1, 2}]

enter image description here

also works.

stevenvh
  • 6,866
  • 5
  • 41
  • 64
  • Regarding the Abs example: try Integrate[If[x > 0, x, -x], x] and now it works. Apparently it assumes a real $x$ for this If[] construct (which a priori I'd have thought shouldn't be used for mathematical functions). – acl Jul 17 '12 at 10:39
  • @acl - "which a priori I'd have thought shouldn't be used for mathematical functions". Exactly my thoughts. It's bad enough that my functions are full of Abs and Max. – stevenvh Jul 17 '12 at 11:14
  • 1
    @acl by implying that $x>0$, it must be real. The same thing occurs when specifying the limits on the integral. – rcollyer Jul 17 '12 at 14:27
  • @acl Complementing rcollyer's answer: see this post. – sebhofer Jul 17 '12 at 14:37
  • @rcollyer but it doesn't, it just says "if x>0". I'm not sure I could have predicted what would happen if I hadn't tried this. – acl Jul 17 '12 at 14:55