Choosing FEM element type and mesh refinement

Question

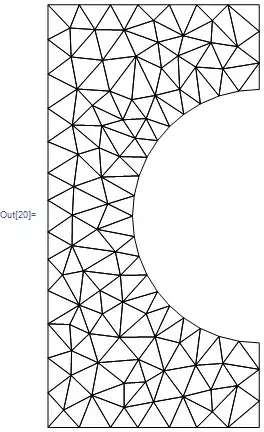
I have only recently been introduced to Mathematica's(v10.0) FEM capabilities. I understand that for solving PDEs on non-uniform shapes via NDSolve, Mathematica uses FEM. I have been able to extract the mesh from some examples shown and I notice that the mesh used by Mathematica is always ordered with equal element sizes. Is there some way I could force NDSolve to choose a combination of quad and tri elements instead of ONLY quad elements or tri elements to solve a PDE? Also is mesh refinement possible (dense mesh in some areas and coarse mesh in others)?

Here's a MWE that I would like to use: It is a notebook file. Forgive the link instead of pasting input text here: the input text was quite garbled and didn't copy back into a Mathematica.

---

update (to copy code from notebook here)

Ω = 
  ImplicitRegion[ ! (x - 5)^2 + (y - 5)^2 <= 3^2, {{x, 0, 5}, {y, 0, 
     10}}]; 
RegionPlot[Ω, AspectRatio -> Automatic]

op = -Laplacian[u[x, y], {x, y}] - 20; 

Subscript[Γ, 
   D] = {DirichletCondition[u[x, y] == 0, x == 0 && 8 <= y <= 10], 
   DirichletCondition[u[x, y] == 100, 
         (x - 5)^2 + (y - 5)^2 == 3^2]}; 

uif = NDSolveValue[{op == 0, Subscript[Γ, D]}, u, 
  Element[{x, y}, Ω], 
     Method -> {"PDEDiscretization" -> {"FiniteElement", 
      "MeshOptions" -> {"MaxCellMeasure" -> 0.3}, 
      "IntegrationOrder" -> 5}}]

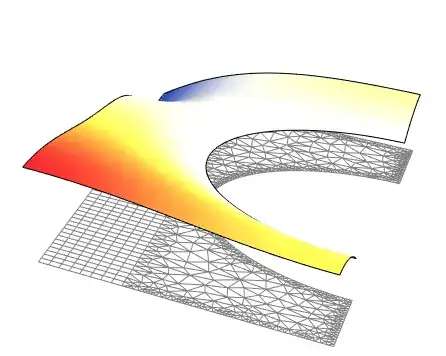
Quiet[ContourPlot[uif[x, y], Element[{x, y}, Ω], 
  ColorFunction -> "Temperature", AspectRatio -> Automatic]]
Plot3D[uif[x, y], Element[{x, y}, Ω], 
 ColorFunction -> "Temperature", AspectRatio -> Automatic, 
 Mesh -> False]

Needs["DifferentialEquations`InterpolatingFunctionAnatomy`"];

{mesh} = InterpolatingFunctionCoordinates[uif]
mesh["Wireframe"]

Answer 1

It's a bit late but here is a way to do it. The idea is to generate a quad mesh from a part of the boundary. The interface to the triangle mesh will be used from the quad mesh and we will generate the triangle mesh without adding Steiner points. This will help us to merge the meshes later into a single mesh.

r1 = Rectangle[{0, 0}, {3/2, 10}];
r2 = RegionDifference[Rectangle[{3/2, 0}, {5, 10}], Disk[{5, 5}, 3]];
Needs["NDSolve`FEM`"]
(leftMesh = ToElementMesh[r1, "MeshOrder" -> 1])["Wireframe"]

Next, we generate a boundary mesh of r2

rightBoundaryMesh = ToBoundaryMesh[r2, "MaxBoundaryCellMeasure" -> 0.1];

The idea is to select the right most edge from the quad mesh and the rest form the right boundary mesh to form a new boundary mesh with the spacing of the boundary elements of the quad mesh on the left edge of the right boundary.

coordinates = 
  Join[Select[leftMesh["Coordinates"], (#[[1]] == 3/2) &], 
   Select[rightBoundaryMesh["Coordinates"], (#[[1]] > 3/2) &]];
incidents = Partition[FindShortestTour[coordinates][[2]], 2, 1];
rightBoundaryMeshNew = ToBoundaryMesh["Coordinates" -> coordinates, 
   "BoundaryElements" -> {LineElement[incidents]}];

Now, we generate a boundary mesh of the right part that uses the boundary element spacing of the quad mesh for the left part. The key point is to use "SteinerPoints" -> False such that no new nodes are introduced on the edges.

rightMesh = 
  ToElementMesh[rightBoundaryMeshNew, "MeshOrder" -> 1, 
   "SteinerPoints" -> False];

rightMesh["Wireframe"]

Note, how on the left edge the quad boundary element spacing is used while on the three remaining edges a "MaxBoundaryCellMeasure" -> 0.1 is used (for illustration).

The last step is to glue the meshes together:

leftCoordinates = leftMesh["Coordinates"];
rightCoordinates = rightMesh["Coordinates"];
mesh = ToElementMesh[
   "Coordinates" -> Join[rightCoordinates, leftCoordinates], 
   "MeshElements" -> 
    Flatten[{rightMesh["MeshElements"], 
      QuadElement /@ (ElementIncidents[leftMesh["MeshElements"]] + 
         Length[rightCoordinates])}]];
mesh["Wireframe"]

This is a first order mesh. You could generate a second order mesh with

MeshOrderAlteration[mesh, 2]

But then you'd need to adjust the mid side nodes of the curved part. Which is certainly doable.

Solve and visualize a PDE:

op = -Laplacian[u[x, y], {x, y}] - 20;
Subscript[\[CapitalGamma], 
   D] = {DirichletCondition[u[x, y] == 0, x == 0 && 8 <= y <= 10], 
   DirichletCondition[u[x, y] == 100, (x - 5)^2 + (y - 5)^2 == 3^2]};
uif = NDSolveValue[{op == 0, Subscript[\[CapitalGamma], D]}, u, 
   Element[{x, y}, mesh]];
Show[
 Plot3D[uif[x, y], Element[{x, y}, mesh], 
  ColorFunction -> "Temperature", AspectRatio -> Automatic, 
  Mesh -> False, Boxed -> False, Axes -> None],
 Graphics3D[{Directive[{EdgeForm[Gray], FaceForm[]}], 
   ElementMeshToGraphicsComplex[mesh, 
    "CoordinateConversion" -> (Join[#, ConstantArray[{0.}, Length[#]],
         2] &)]}]
 ]