plot randomly oriented lines

Question

I want to create the following graphic:

A set of line-elements are randomly oriented in planes parallel to xy-plane. In addition, on each plane the drawed line-elements should not cross each other. Also, the magnitude of these line-elements is not constant.

How is it possible to create the figure?

Thank you very much.

Did you try anything yet? The hard part will be the non-crossing thing. — Yves Klett, May 19 '15 at 14:06
For a start, try Line[{{RandomReal[],RandomReal[],z},{RandomReal[],RandomReal[],z}}]/.z->RandomReal[] — LLlAMnYP, May 19 '15 at 14:07
@YvesKlett non-crossing appears to be trivial enough. line1=RegionMember[Line[{{...}}],{x,y,z}];line2=RegionMember...; then Reduce[line1&&line2]. If it comes up with a solution, then they cross. — LLlAMnYP, May 19 '15 at 14:17
Do you want the the planes to be discrete,for example random integer zs? Because with float random numbers of @LLlAMnYP 's comment, it's highly, highly unlikely that two lines will end up in the same plane. — egwene sedai, May 19 '15 at 14:18
Thanks for the answers. @egwenesedai. Yes, if for instance, 100 lines are drawed in total I want several of them to appear on the same plane. — Dimitris, May 19 '15 at 14:21
@LLlAMnYP nice - how would that fare performance-wise for many lines that need to be compared? — Yves Klett, May 19 '15 at 14:25
@YvesKlett: What I have tried so far have been done with ParametricPlot3D. But nothing sophisticated. And certainly no truly randomly:-)! — Dimitris, May 19 '15 at 14:29
@YvesKlett actually the performance is surprisingly good even without coding an analytical approach: lines = Partition[RandomReal[1, {100, 2}],2]; Solve[RegionMember[Line[First@lines], {x, y}] && RegionMember[Line[#], {x, y}]] & /@ Rest[lines] // AbsoluteTiming — LLlAMnYP, May 19 '15 at 14:47
@dimitris If you would care to define the problem as specifically as possible, that is, including constraints on coordinates, at what z coordinates you would like the lines to lie, how many lines per plane, anything of that sort that comes to your mind, I'd give it a shot. — LLlAMnYP, May 19 '15 at 14:51
If you have the time, give it a try. I don't have something particular in my mind. I just want to reproduce a fiber-reinforced composite with fibers randomly oriented in planes parallel to xy-plane. The requirements are different length of these line elements, different orientation and certainly non-crossing which is a physical requirement. If you don't have the time, for me it suffices the combination of the previous codes. — Dimitris, May 19 '15 at 14:59
For instance: How it will be used the output of lines = Partition[RandomReal[1, {100, 2}],2]; Solve[RegionMember[Line[First@lines], {x, y}] && RegionMember[Line[#], {x, y}]] & /@ Rest[lines] — Dimitris, May 19 '15 at 15:07
You might want to see this for a way to check line intersections. — J. M.'s missing motivation, May 19 '15 at 15:27

LLlAMnYP · Accepted Answer · 2015-05-19T15:30:29.763

2

This is not a full answer, but it, perhaps, deals with the hardest part: constructing a set of finite lines lying all in one plane, but not intersecting each other.

appendLine[list_Symbol] := (list = RandomReal[10, {1, 2, 2}])
appendLine[list_List] := Module[{newline, test = True},
  For[newline = RandomReal[10, {2, 2}], test, 
   test = ! 
     AllTrue[Solve[
         RegionMember[Line[newline], {x, y}] && 
          RegionMember[Line[#], {x, y}]] & /@ list, Length@# == 0 &], 
   newline = RandomReal[10, {2, 2}]];
  Append[list, newline]]

Run list = appendLine[list] n times to get n lines:

Do[list = appendLine[list], {n, 20}] // AbsoluteTiming
(* {4.099410, Null} *) <- (* quite slow for only 20 lines, unfortunately *)

Display:

Graphics[Line /@ list]

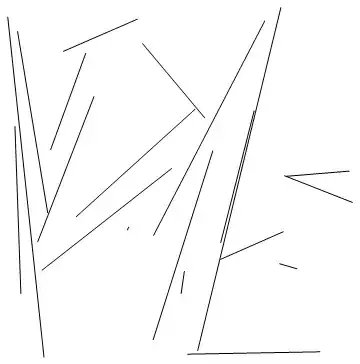
It's a cool model system to study, how depending on initial conditions, for example, all lines mostly orient themselves along a specific direction.

PS - a subsequent addition of 20 lines took 26 seconds, and the next line took another 1.4. Makes sense, as each new random line is more and more likely to intersect the previous ones, so more and more attempts to generate a new line need to be made, until one comes up that fits.

edited May 19 '15 at 15:30

answered May 19 '15 at 15:15

LLlAMnYP

11,486
26
65

I cannot reproduce the results. Graphics[Line /@ list] results in one line. Graphics[Line /@ line] results in two lines even modifying n. – Dimitris May 19 '15 at 15:28
Crap, typo. line->list of course. Will fix – LLlAMnYP May 19 '15 at 15:29
@dimitris now it should work – LLlAMnYP May 19 '15 at 15:31
For[], huh? I'd probably have used While[] instead; also, you might be interested in the undocumented function for checking line intersections. – J. M.'s missing motivation May 19 '15 at 15:33
Yes it works. Thanks. – Dimitris May 19 '15 at 15:33
@Guesswhoitis. the FindIntersections function is undoubtedly pure win :) Maybe I'll get round to updating my answer later. As for For or While - I don't know, can it really make a difference with an implementation like this? Admittedly, While is cleaner. What I was looking for, however, is a repeat-until construct. – LLlAMnYP May 19 '15 at 16:46
I was actually alluding to IntersectQ[], but I'm told these goodies are now in a different context. With respect to looping, have you seen this? (All that's needed is to flip the polarity of the termination criterion.) – J. M.'s missing motivation May 19 '15 at 17:14
No, flipping the polarity is not necessary, as the docs show, all thats needed is the replacement of < with <= or post-increment to pre-increment and so on. But I generally don't use looping constructs often, so this was something new to learn for me. – LLlAMnYP May 19 '15 at 18:00
Oh right; for some reason I had thought you were doing "repeat-until". Got confused there… :) – J. M.'s missing motivation May 19 '15 at 18:25
Yeah, I was looking for a repeat-until, but had to do otherwise. – LLlAMnYP May 19 '15 at 18:44

plot randomly oriented lines

1 Answers1

Linked