Fitting data to plot using errors as weights

Question

I have some enzyme kinetics data that I want to fit to the Michaelis-Menten curve in order to obtain the kinetic parameters of the enzyme.

Is it meaningful, statistically and functionally speaking, to use the error bars (standard deviation) of the measurements as weights in the NonlinearModelFit function, and are there any caveats that I need to take note of when using the function this way?

Needs["ErrorBarPlots`"]
rateList = 
  Transpose[{{0, 0.1, 0.3, 0.5, 1, 3, 10}, {0, 0.0107, 0.0179, 
     0.02103, 0.0314, 0.0645, 0.0875}}];
errorList = {0.0015, 0.00043, 0.00071, 0.0043, 0.0051, 0.0050, 0.0071};
weightList = 1/errorList;
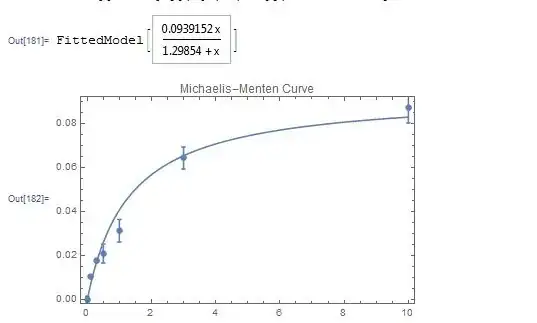
mmfit = NonlinearModelFit[rateList, a*x/(b + x), {a, b}, x, 
  Weights -> weightList]
Show[ErrorListPlot[
  Table[{rateList[[i]], ErrorBar[errorList[[i]]]}, {i, 
    Length[rateList]}], AxesLabel -> {"[Substrate] (mM)", "Activity (Units)"},
   PlotLabel -> "Michaelis-Menten Curve"], 
 Plot[{mmfit[x]}, {x, 0, 10}], Frame -> True]

Also, the AxesLabel property of the plot does not seem to be displaying the axes' names in the resulting plot. What am I doing wrong in this case that is preventing the axes from being correctly displayed?

enter image description here

The standard practice, as noted here, is to weight by variance; so, weightList = 1/errorList^2 seems more appropriate. — J. M.'s missing motivation, May 21 '15 at 19:19
You have set Frame to True so you need FrameLabels rather than AxesLabels. — Sjoerd C. de Vries, May 21 '15 at 19:19
@Guesswhoitis. After changing my weights to use the square of the standard deviations, the curve is now cut off. I presume this is again due to some automated plot shenanigans near an asymptote, but I can't find the correct option to use in the Plot documentation to fix this. — March Ho, May 21 '15 at 20:02
Put the Plot[] first in your Show[], and move the options in ErrorListPlot[] out as options to Show[]. — J. M.'s missing motivation, May 21 '15 at 20:07
... or, possibly more easily, just add PlotRange->Full to the Plot function. — MarcoB, May 21 '15 at 20:10

Fitting data to plot using errors as weights

0 Answers0