-3

I am interested in this definite integral:

$$ \eqalign{\int_0^\infty {x^2 \log(1-e^{-x})}\; dx\cr } $$

That is:

Integrate[x^2 Log[(1 - Exp[-x])], {x, 0, \[Infinity]}]

Mathematica outputs a nice result:

$-\frac{\pi ^4}{45}$

But is there any way for users like me to see what actual symbolic calculations were performed by Mathematica in order to get the result?

Using WolframAlpha:

There is a possibility of using WolframAlpha, like here:

WolframAlpha["Integrate[Sin[x]*Sin[x]], {x,0,\[Pi]}]", 
 IncludePods -> "Input", AppearanceElements -> {"Pods"}, 
 PodStates -> {"Show steps"}]

This is the output, which is really nice, I was impressed, it's almost like written by a human: (the only missing thing is some "handwriting" font ;) )

enter image description here

However, for my case, steps are not offered:

WolframAlpha["Integrate[x^2 Log[(1 - Exp[-x])], {x,0,\[Infinity]}]", 
 IncludePods -> "Input", AppearanceElements -> {"Pods"}, 
 PodStates -> {"Show steps"}]

enter image description here

Graph of the function:

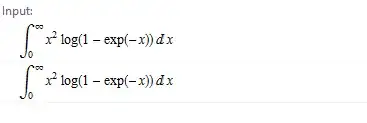
enter image description here

VividD
  • 3,660
  • 4
  • 26
  • 42
  • Did you try searching for duplicates ? (148) – Sektor May 24 '15 at 15:08
  • @Sektor Do you see my example in the question you linked to? – VividD May 24 '15 at 15:11
  • 2
    Maybe you can look at Rubi, but I am not sure that thing knows about zeta functions or polylogarithms, which will more than likely pop up in the evaluation of this integral. – J. M.'s missing motivation May 24 '15 at 15:18
  • 1
    Sometimes using = to pass a result to WolframAlpha, expanding what is returned and selecting Show Steps can give you some steps, but for this and other complicated integrals there are often no steps available. Sometimes doing the indefinite integral, plotting that and looking at each term in the result evaluated at lower and upper bound can give some clues. That gives a few hints here, but not all the details you are asking for. – Bill May 24 '15 at 16:02
  • @J. M. Thanks for the hint. Rubi does seem to be too helpful. It doesn't handle definite integrals (or I don't know how to use it for that purpose). Correspondent indefinite integral is a complex expression involving polylogs, and the tricky part is reducing definite integral from the question to clean -pi^4/45. Are you saying that there is no way to expose Mathematica's internal steps to -pi^4/45? – VividD May 24 '15 at 16:07
  • 2
    Well, internally, Mathematica uses a heavily modified (and proprietary!) version of the Risch algorithm, expanded to include things like exponential integrals and polylogarithms. That approach will certainly not be the way a human might go about it. I'm not even sure if Mathematica knows things like Landen's identity… – J. M.'s missing motivation May 24 '15 at 16:32
  • To add an example close to my heart: the usual result of Mathematica's evaluation of an elliptic integral is something that is correct, but somewhat useless (too complicated, involves complex numbers when the result is supposed to be real); on the other hand, someone with sufficient stamina and a copy of Byrd/Friedman close by will likely be able to produce a cleaner elliptic integral expression. So, with things like these, I'm not optimistic about getting Mathematica to show its nasty guts. – J. M.'s missing motivation May 24 '15 at 16:37
  • @J. M. I guess than the only hope is something external like Rubi or Wolfram. Thanks for your time, I appreciate your opinion. – VividD May 24 '15 at 16:40
  • @Bill I appreciate you hint. I updated the question with Wolfram approach. However, it didn't like my integral. Did I do everything right? – VividD May 24 '15 at 16:43
  • Since I mentioned Landen anyway… you might want to see this. – J. M.'s missing motivation May 26 '15 at 11:31
  • @J. M. Great find, very interesting area, thank you! – VividD May 26 '15 at 18:00

1 Answers1

4

As stated in the OP Mathematica finds this value of the integral within seconds

f0 = Integrate[x^2 Log[1 - E^-x], {x, 0, \[Infinity]}]

(*
Out[21]= -(\[Pi]^4/45)
*)

Most probably Mathematica employs this standard procedure:

1) solve the indefinte integral, i.e. find an antiderivative
2) check continuity of the antiderivative
3) use the fundamental theorem of calculus, i.e. find the difference of the antiderivative in the two ends of the integration interval

Step 1: find antiderivative fi

fi = Integrate[x^2 Log[1 - E^-x], x]

(*
Out[9]= 1/12 (x^4 + 4 x^3 Log[1 - E^-x] - 4 x^3 Log[1 - E^x] - 
   12 x^2 PolyLog[2, E^x] + 24 x PolyLog[3, E^x] - 24 PolyLog[4, E^x])
*)

Step 2: check continuity

Let's do this graphically

Plot[fi, {x, 0, 9}, PlotRange -> {-2, -5}, 
 PlotLabel -> 
  "Antiderivative fi of \!\(\*SuperscriptBox[\(x\), \
\(2\)]\)Log[1-\!\(\*SuperscriptBox[\(\[ExponentialE]\), \(-x\)]\)]", 
 AxesLabel -> {"x", "fi"}]
(* 150526_plot_fi.jpg *)

enter image description here

Check was affirmative.

Step 3: evaluate antiderivative at interval ends

fi /. x -> 0

During evaluation of In[19]:= Infinity::indet: Indeterminate expression 0 (-[Infinity]) encountered. >>

(*   
Out[19]= Indeterminate
*)

Ok, so we must take the limit

fiLow = Limit[fi, x -> 0]

(*
Out[16]= -(\[Pi]^4/45)
*)

fiUp = Limit[fi, x -> \[Infinity]]

(*
Out[17]= -((2 \[Pi]^4)/45)
*)

Final result

f = fiUp - fiLow

(*
Out[20]= -(\[Pi]^4/45)
*)

which is identical to f0.
Done.

Dr. Wolfgang Hintze
  • 13,039
  • 17
  • 47