A problem with Manipulate

Question

I have:

Clear[f, a, b, n, dx];
f[x_] = x^2;
a = 0; b = 1; dx = (b - a)/n;
Manipulate[
 Show[Plot[f[x], {x, a, b},
   PlotStyle -> Thick,
   AxesLabel -> {x, y}],
  Graphics[{
    Table[
     {Opacity[0.05], EdgeForm[Gray],
      Rectangle[{a + i dx, 0}, {a + (i + 1) dx, f[a + i dx]}]}, {i, 0,
       n - 1, 1}]
    }]],
 {{n, 10}, 10, 50, 10}
 ]

But I get an error:

Coordinate {$CellContext`n^(-1), 0} should be a pair of numbers, or a Scaled or Offset form.

Can someone tell me what I am doing wrong?

Thanks to Mahdi, I now have:

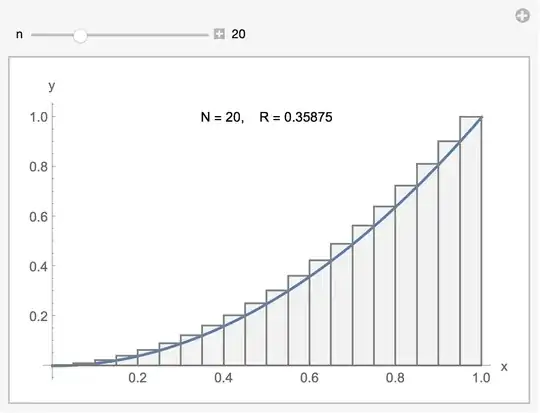
Manipulate[Module[{a = 0, b = 1, dx, f, rightSum},
  dx = (b - a)/n;
  f[x_] = x^2;
  rightSum = N@Sum[f[a + i dx] dx, {i, 1, n}];
  Show[Plot[f[x], {x, a, b},
    PlotStyle -> Thick,
    AxesLabel -> {"x", "y"}],
   Graphics[{
     Table[{Opacity[0.05], EdgeForm[Gray], 
       Rectangle[{a + i dx, 0}, {a + (i + 1) dx, 
         f[a + (i + 1) dx]}]}, {i, 0, n - 1, 1}],
     Text[
      "N = " <> ToString[n] <> ",    R = " <> 
       ToString[rightSum], {(a + b)/2, f[b]}]
     }]]],
 {{n, 10}, 10, 50, 10, Appearance -> "Labeled"}]

Which produces this image:

enter image description here

Couple things I learned:

I tried:

Module[{a = 0, b = 1, dx=(b-a)/n, f, rightSum}

It worked, but when I changed the b=1 to a b=2, it did not work. So, apparently the dx=(b-a)/n does not use the b=1 in the module.

On the other hand, when I put it inside the module,

Manipulate[Module[{a = 0, b = 1, dx, f, leftSum}, dx = (b - a)/n;

it worked.

Thus far, I have two manipulates in my notebook, which don't seem to interfere with one another or all of the static code I have in the notebook.

Difficulty with Initialization: After reading Martin John Hadley's comment, I tried the following:

Manipulate[
 Show[Plot[f[x], {x, a, b},
   PlotStyle -> Thick,
   AxesLabel -> {"x", "y"}],
  Graphics[{
    Table[{Opacity[0.05], EdgeForm[Gray], 
      Rectangle[{a + i dx[n], 0}, {a + (i + 1) dx[n], 
        f[a + i dx[n]]}]}, {i, 0, n - 1}],
    Text["N = " <> ToString[n] <> ",    L = " <> 
      ToString[leftSum], {(a + b)/2, f[b]}]
    }]],
 {{n, 10}, 10, 50, 10, Appearance -> "Labeled"},
 Initialization :> (
   dx[n_] := (b - a)/n;
   f[x_] = x^2;
   leftSum = N@Sum[f[a + i dx[n]] dx[n], {i, 0, n - 1}];
   a = 0;
   b = 2
   )]

But it didn't work. I got errors such as:

Coordinate {Rational[1, 5][10], 0} should be a pair of numbers, or a Scaled or Offset form.

I cannot determine what is wrong here? Any thoughts?

Answer to my Own Question: I should have put a=0 and b=2 as the first two lines in the initialization block.

Final Result due to help from Martin John Hadley:

Manipulate[
 Show[Plot[f[x], {x, a, b}, PlotStyle -> Thick, 
   AxesLabel -> {"x", "y"}], 
  Graphics[{Table[{Opacity[0.05], EdgeForm[Gray], 
      Rectangle[{a + i dx[n], 0}, {a + (i + 1) dx[n], 
        f[a + (i + 1) dx[n]]}]}, {i, 0, n - 1, 1}], 
    Text["N = " <> ToString[n] <> ",    R = " <> 
      ToString[rightSum[n]], {(a + b)/2, f[b]}]}]], {{n, 10}, 10, 50, 
  10, Appearance -> "Labeled"},
 Initialization :> (a = 0; b = 1; dx[n_] := (b - a)/n; f[x_] := x^2;
   rightSum[n_] := N@Sum[f[a + i dx[n]] dx[n], {i, 1, n}])]

And the output image:

enter image description here

Thanks to both Martin and Mahdi for tremendous help.

David, the final result is so nice! Also, it worked for $b = 1$ because you had it globally before. Start a new notebook and run this: Module[{a = 1, b = 1, n = 1, dx = (b - a)/n}, Print[dx]], you clearly see that in dx = (b - a)/n, b,a, and n are blue (not green)! And the code returns (-a+b/n). — Mahdi, May 25 '15 at 17:30
@Mahdi: Very helpful. I do see that a, b, and n were not used when assigning (b-a)/n to dx. However, green means what in this example? And blue means what in this example? — David, May 25 '15 at 19:20
Blue is for symbols with no assigned values, green is for local variables. Of course, these are default colors for Mathematica and you can modify colors (and find their meanings) under Edit>Preferences>Appearance. — Mahdi, May 25 '15 at 20:45

score 4 · Accepted Answer · edited Apr 13 '17 at 12:55

As mentioned in my comment on Mahdi's answer, it is generally not advisable to use Module within Manipulate - https://mathematica.stackexchange.com/a/80324/1952 gives a good explanation of why.

I have refactored your code into a Manipulate that uses Initialization, as advised by Mahdi it is necessary to change your definition of f to use SetDelayed rather than Set and I also created a function dx dependent on the variable n:

Manipulate[
 Show[Plot[f[x], {x, a, b}, PlotStyle -> Thick, 
   AxesLabel -> {"x", "y"}], 
  Graphics[{Table[{Opacity[0.05], EdgeForm[Gray], 
      Rectangle[{a + i dx[n], 0}, {a + (i + 1) dx[n], 
        f[a + (i + 1) dx[n]]}]}, {i, 0, n - 1, 1}]}]],
 {{n, 10}, 10, 50, 10, Appearance -> "Labeled"},
 Initialization :> (
   a = 0; b = 1; dx[n_] := (b - a)/n; f[x_] := x^2; 
   rightSum[n_] := N@Sum[f[a + i dx[n]] dx[n], {i, 1, n}]
   )
 ]

Edit

My initial DynamicModule solution did not work in a clean kernel due to the same issue I helped someone with recently, content in Initialization is not evaluated until after the construct is first displayed - https://mathematica.stackexchange.com/a/80767/1952.

I've modified the DynamicModule to assign a and b within the variable specification and f within the body of the DynamicModule

 DynamicModule[{n, a = 0, b = 1, f},
 f[x_] := x^2;
 Panel[Column[
   {
    Control[{n, 10, 50, 10}], 
    Show[Plot[f[x], {x, a, b}, PlotStyle -> Thick, 
      AxesLabel -> {"x", "y"}, ImageSize -> 500], 
     Graphics[{Dynamic@
        Table[{Opacity[0.05], EdgeForm[Gray], 
          Rectangle[{a + i dx[n], 0}, {a + (i + 1) dx[n], 
            f[a + (i + 1) dx[n]]}]}, {i, 0, n - 1, 1}]}]]
    }
   ]
  ], Initialization :> (dx[n_] := (b - a)/n; 
   rightSum[n_] := N@Sum[f[a + i dx[n]] dx[n], {i, 1, n}])]

Looks like a minor error here. Shouldn't the last line in each code module be rightSum[n_] := N@Sum[f[a + i dx[n]] dx[n], {i, 1, n}]? Also, I added your code to my original post above, plus I put in my title. Thanks for the marvelous help. — David, May 25 '15 at 20:31
@David sorry about that oversight, glad you caught it and I've edited my answer, also note the change to the DynamicModule. Very glad to have helped out :) — Charlotte Hadley, May 25 '15 at 21:24
@MartinJohnHadley: See http://mathematica.stackexchange.com/questions/84378/continuation-of-a-problem-with-manipulate for a continuation of this problem. I can't create notebooks for my students with numerous Manipulates and other static stuff if I am just using this Initialization idea. However, I would like to again thank you for your help. — David, May 25 '15 at 21:39
@David I'll take a look tomorrow evening if there's been no answer — Charlotte Hadley, May 25 '15 at 21:43

Mahdi · Answer 2 · 2015-05-25T09:09:29.117

3

You need to specify dx as a function of n, or replace dx definition directly in Manipulate.

Functional Form of dx

Clear[f, a, b, n, dx];
f[x_] := x^2;
a = 0; b = 1;
dx[n_] := (b - a)/n;
Manipulate[
 Show[Plot[f[x], {x, a, b}, PlotStyle -> Thick, 
   AxesLabel -> {"x", "y"}], 
  Graphics[{Table[{Opacity[0.05], EdgeForm[Gray], 
      Rectangle[{a + i dx[n], 0}, {a + (i + 1) dx[n], 
        f[a + i dx[n]]}]}, {i, 0, n - 1, 1}]}]
  ], {{n, 10}, 10, 50, 10}]

Local variables within Manipulate

To have a,b and f as local variables, you could use Module:

Manipulate[
 Module[{a = 0, b = 1, f},
  f[x_] := x^2;
  Show[Plot[f[x], {x, a, b}, PlotStyle -> Thick, 
    AxesLabel -> {"x", "y"}], 
   Graphics[{Table[{Opacity[0.05], EdgeForm[Gray], 
       Rectangle[{a + i (b - a)/n, 0}, {a + (i + 1) (b - a)/n, 
         f[a + i (b - a)/n]}]}, {i, 0, n - 1, 1}]}]]
  ], {{n, 10}, 10, 50, 10}]

Both methods result in the following:

enter image description here

edited May 25 '15 at 09:09

answered May 25 '15 at 07:24

Mahdi

1,619
10
23

Nice explanation. Can you show me how to place the dx definition directly in manipulate? – David May 25 '15 at 08:02
Could you also show me how you would define a, b, and f[x_] in Manipulate so that they don't use what is currently in the Global workspace, nor do they add anything to the Global workspace. Thanks. – David May 25 '15 at 08:03
1

Thank you @David! Please see my edit! – Mahdi May 25 '15 at 08:24
1

I've added some of your technique to my original post up above. So far, two Manipulate animations are not interfering with one another or static items in the workspace. Thanks for your help. – David May 25 '15 at 17:23
2

Generally not advisable to use Module within Manipulate, see http://mathematica.stackexchange.com/a/80324/1952. You would be better looking at Initialisation or else DynamicModule. – Charlotte Hadley May 25 '15 at 17:35
@MartinJohnHadley: I can't handle dynamic at this point. Not a beginner, but not intermediate yet either. I would really appreciate it if you could add an answer with your initialization suggestion, so that the Manipulate activity does not use or change a, b, dx, f, or rightSum from the Global workspace. It would be extremely helpful! Thanks. – David May 25 '15 at 18:24
@MartinJohnHadley: I added your thoughts to my example in my original post up above, but I am struggling to make it work. Any thoughts? – David May 25 '15 at 19:23

A problem with Manipulate

2 Answers2

Linked