List operations: how to combine two lists (pattern given)?

Question

Two lists (matrixes) are given:

a = {{x1, y1}, {x2, y2}, {x3, y3}};
b = {{u1, v1}, {u2, v2}, {u3, v3}};

Expected return:

c = {{{x1, u1}, {y1, v1}}, {{x2, u2}, {y2, v2}}, {{x3, u3}, {y3, v3}}}

Please, help to solve this. Useful references are also welcome.
Added:

duplicates

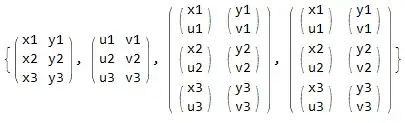
Have a look at ArrayFlatten[] or MapThread[] and Transpose[]. — J. M.'s missing motivation, May 26 '15 at 16:24

score 4 · Accepted Answer · answered May 26 '15 at 16:26

4

MapThread can solve this.

a = {{x1, y1}, {x2, y2}, {x3, y3}};
b = {{u1, v1}, {u2, v2}, {u3, v3}};
c = MapThread[List, #] & /@ MapThread[List, {a, b}]

The output is

{{{x1, u1}, {y1, v1}}, {{x2, u2}, {y2, v2}}, {{x3, u3}, {y3, v3}}}

answered May 26 '15 at 16:26

Purboo

677
3
15

6

even shorter: MapThread[List, {a, b}, 2] – chuy May 26 '15 at 16:29
1

Even harder to read: Transpose@{#1,#2}&@@@Transpose@{a,b} :) – N.J.Evans May 26 '15 at 16:34
My fault not to think and search carefully before asking. Nice general way: SetAttributes[add, Listable]; add[x_,y_]:={x,y} – garej May 26 '15 at 19:52

score 2 · Answer 2 · answered Feb 22 '24 at 09:45

2

a = {{x1, y1}, {x2, y2}, {x3, y3}};
b = {{u1, v1}, {u2, v2}, {u3, v3}};
c = {{{x1, u1}, {y1, v1}}, {{x2, u2}, {y2, v2}}, {{x3, u3}, {y3, v3}}}

res = Thread[{a, b}] // Transpose[#, {1, 3, 2}] &

MatrixForm /@ {a, b, c, res}

answered Feb 22 '24 at 09:45

Syed

52,495
4
30
85

score 2 · Answer 3 · answered Feb 22 '24 at 10:05

2

a = {{x1, y1}, {x2, y2}, {x3, y3}};
b = {{u1, v1}, {u2, v2}, {u3, v3}};

Transpose /@ Transpose[{a, b}]

{{{x1, u1}, {y1, v1}}, {{x2, u2}, {y2, v2}}, {{x3, u3}, {y3, v3}}}

answered Feb 22 '24 at 10:05

eldo

67,911
5
60
168

gwr · Answer 4 · 2024-02-22T11:39:25.767

2

As of Version 13.1+, we could use Threaded like so:

a = {{x1, y1}, {x2, y2}, {x3, y3}};
b = {{u1, v1}, {u2, v2}, {u3, v3}};
combine = Function[{e1, e2}, {e1, e2}, Listable];
a ~ combine ~ Threaded @ b
(* {{{x1,u1},{y1,v1}},{{x2,u2},{y2,v2}},{{x3,u3},{y3,v3}}} *)

But in this case it isn’t even needed as we are operating at the lowest level for two lists having the same dimensions:

a ~ combine ~ b

edited Feb 22 '24 at 11:39

answered Feb 22 '24 at 11:23

gwr

13,452
2
47
78

Of course, combine[ a, Threaded[b] ] is equivalent. – gwr Feb 22 '24 at 11:25

score 2 · Answer 5 · answered Feb 22 '24 at 14:20

2

Transpose[{a, b}, {3, 1, 2}]

{{{x1, u1}, {y1, v1}}, {{x2, u2}, {y2, v2}}, {{x3, u3}, {y3, v3}}}

answered Feb 22 '24 at 14:20

Karl

941
1
7

E. Chan-López · Answer 6 · 2024-02-22T13:43:37.400

1

a = {{x1, y1}, {x2, y2}, {x3, y3}};
b = {{u1, v1}, {u2, v2}, {u3, v3}};

Using Riffle, Partition and Thread:

Thread /@ Partition[Riffle[a, b], 2]
({{{x1, u1}, {y1, v1}}, {{x2, u2}, {y2, v2}}, {{x3, u3}, {y3, v3}}})

Or using Table, Partition and Riffle:

Table[Partition[Riffle[a[[i]], b[[i]]], {2}], {i, #}] &@ Max@Dimensions@{a, b}
({{{x1, u1}, {y1, v1}}, {{x2, u2}, {y2, v2}}, {{x3, u3}, {y3, v3}}})

edited Feb 22 '24 at 13:43

answered Feb 22 '24 at 13:34

E. Chan-López

23,117
3
21
44

ben · Answer 7 · 2015-05-27T14:05:42.550

1

Map[Variables,Partition[Flatten[a]*Flatten[b], 1]]

outputs

{{u1,x1}, {v1,y1}, {u2,x2}, {v2,y2}, {u3,x3}, {v3,y3}}

The Documentation Center is a great resource.

edited May 27 '15 at 14:05

answered May 26 '15 at 21:31

ben

97
4

Thank U, I've noticed that DC has a direct solution to my 'problem'. BTW, output is not exactly as expected. – garej May 27 '15 at 05:53

List operations: how to combine two lists (pattern given)?

7 Answers7