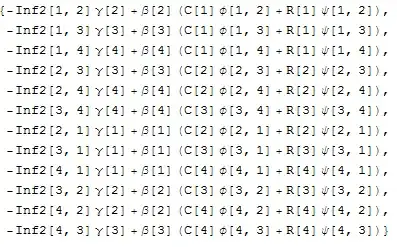4

NOTE: This question is very similar to this one but I realized reading at the answers that I made a mistake in the equation AND I was not clear enough about what I need (my apologies):

I want to evaluate this expression:

expr1[i_,j_] = β[j]*ϕ[i, j]* C[i]

For $i=1:4, \, j=1:4$ with $i \ne j$, so over this list of tuples:

A = {{1, 2}, {1, 3}, {1, 4}, {2, 1}, {2, 3}, {2, 4}, {3, 1}, {3, 2}, {3, 4}, {4, 1}, {4, 2}, {4, 3}}.

so that I get:

expr1[1,2] = β[2]*ϕ[1,2]*C[1]
expr1[1,3] = β[3]*ϕ[1,3]*C[1]
...
expr1[4,3] = β[3]*ϕ[4,3]*C[4]

I have tried the following code:

expr2ind[i_, j_] := 
dInf2[i, j] = β[
 j]*(ψ[i, j] Boole[i != j]* 
   R[i] + ϕ[i, j] Boole[i != j]* C[i]) - γ[j]*
Inf2[i, j] Boole[i != j]

Do[expr2ind[i, j][[1]]; 
CellPrint@Cell[BoxData@ToBoxes@expr2ind[i, j], "Input"], {i, 1, 
4}, {j, 1, 4}]

This works well, except for the fact that the "Do" loop still computes the pairs (i,i), getting the following message: Part::partd: Part specification 0[1] is longer than depth of object. >>

and getting a 

0

which I am trying to avoid. Basically, I want to know if there is a way to iterate over a particular set of tuples in Mathematica, equivalent to Python or Matlab. Thanks

Community
  • 1
Laura
  • 167
  • 4

3 Answers3

3
expr1 @@@ DeleteCases[Tuples[Range @ 4, {2}], {a_, a_}]

{C[1] β[2] ϕ[1, 2], C[1] β[3] ϕ[1, 3], C[1] β[4] ϕ[1, 4], C[2] β[1] ϕ[2, 1], C[2] β[3] ϕ[2, 3], C[2] β[4] ϕ[2, 4], C[3] β[1] ϕ[3, 1], C[3] β[2] ϕ[3, 2], C[3] β[4] ϕ[3, 4], C[4] β[1] ϕ[4, 1], C[4] β[2] ϕ[4, 2], C[4] β[3] ϕ[4, 3]}

where @@@ is a shortcut for Apply at level {1}.

If your intention is to define expr1 for the input tuples it would be:

(expr1[#1,#2]=β[#2]*ϕ[#1, #2]* C[#1])& @@@ 
  DeleteCases[Tuples[Range @ 4, {2}], {a_, a_}]
m_goldberg
  • 107,779
  • 16
  • 103
  • 257
Sjoerd C. de Vries
  • 65,815
  • 14
  • 188
  • 323
  • Thanks, could you please explain the difference between the first and the second options? It is not obvious to me. – Laura May 27 '15 at 18:16
  • The first option literally does what's in the title of your question: it evaluates a function over a set of tuples. Your question body itself seemed to suggest that you wanted to set (define) expr[1,1], expr[1,2] etc. So, this is what the second option does. It uses a pure function to do this. – Sjoerd C. de Vries May 27 '15 at 18:54
2
expr2ind[i_, j_] := β[j](ψ[i, j] Boole[i != j] R[i] +
     ϕ[i, j] Boole[i != j] C[i]) - γ[j] Inf2[i, j] Boole[i != j]

pairs = Join @@ {#, Reverse /@ #} &@Subsets[Range[4], {2}];
expr2ind @@@ pairs

enter image description here

Sum[expr2ind @@ k, {k, pairs}]

enter image description here

kglr
  • 394,356
  • 18
  • 477
  • 896
0

Changing the arguments in your function to a list...

expr1[{i_, j_}] := β[j]*ψ[i, j]*C[i]
Map[expr1[#] &, Subsets[Range[4], {2}]] // TableForm

C[1] β[2] ψ[1,2]
C[1] β[3] ψ[1,3]
C[1] β[4] ψ[1,4]
C[2] β[3] ψ[2,3]
C[2] β[4] ψ[2,4]
C[3] β[4] ψ[3,4]

Subsets will avoid repeating the same index in the argument of expr1.

ben
  • 97
  • 4