7

Bug introduced in 8.0 or earlier and fixed in 10.4

I'm working on this SE question about pentagrams on top of dodecahedron for exercising. Both solutions are basically connecting different sets of vertices of existing dodecahedron. They don't really deal with carving. I want to build a new polyhedron having pentagrams as faces.

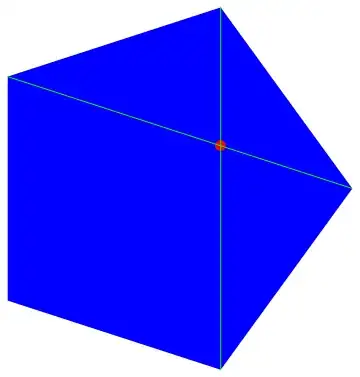
I started with a 2D Pentagon and calculated vertices of pentagram from existing vertices of pentagon:

 penPts = {Cos[#], Sin[#]} & /@ Range[0, 2 Pi, 2 Pi/5][[1 ;; -2]];

 tau = (2 Sqrt[5])/(5 + Sqrt[5]);

 Graphics[{Blue, Polygon[penPts], Red, PointSize [0.03],   
 Point[penPts[[2]]*tau + penPts[[5]]*(1 - tau)], Green,   
 Line[penPts[[{1, 3}]]], Line[penPts[[{2, 5}]]]}]

Finding "inner" vertex of pentagram

Then I defined a function that takes a list of pentagon vertices and makes a list of pentagram vertices:

pentagram[pts_] := 
  Riffle[pts, #] &@(pts[[# + 1]]*tau + (1 - tau)*
        pts[[1 + Mod[# + 2, 5]]] & /@ Range[0, 4, 1]);


Graphics[{Red, PointSize [0.03], Point[pentagram[penPts]], Green, 
  Opacity[0.5], Polygon[pentagram[penPts]]}]

Building 2D pentagram

Since it finds additional vertices by linear combination of existing ones (using tau and (1-tau) as weights) it will work for 3D points as well.

ind = PolyhedronData["Dodecahedron", "FaceIndices"];
vert = PolyhedronData["Dodecahedron", "VertexCoordinates"];
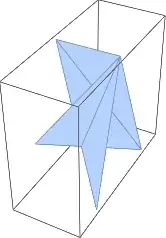
Graphics3D[ Polygon /@ pentagram /@ (vert[[#]] & /@ ind)]

It kinda worked out. The problem is that not all faces are shown as pentagrams, actually only two of them are pentagrams and all other have nasty artifact. See picture. enter image description here

I can see that the only two faces that worked out are parallel to coordinate plane. So my guess is that the calculations were more accurate there. Other faces suffered the fact that the calculated vertices were not actually in one plane.

Question: Is this correct? If so, what can be done to get rid of artifacts (I know I can triangulate them to make unflatness "invisible")?

Community
  • 1
BlacKow
  • 6,428
  • 18
  • 32
  • A sketch: find the normal to the plane of a face, use that to rotate the face so that the face is parallel to a coordinate plane (one of the components becomes zero), work out your transformation there, and then rotate back. – J. M.'s missing motivation Jun 02 '15 at 22:13
  • As for computing the normal of a face, use the newellNormals[] routine from here. – J. M.'s missing motivation Jun 02 '15 at 22:19
  • You are basically suggesting to make a pentagram in 2D and replicate it with appropriate transformations. But the resulting polygons will be all independent, they won't share vertices as they do now. So it will be workaround for particular case for visualization purpose. I'm trying to figure out how to force mathematica to draw my set of points correctly. Also all coordinates can be calculated with arbitrary precision. How can I specify tolerance for a point to belong to a plane? – BlacKow Jun 03 '15 at 02:53
  • Calculating normal is straightforward in my case: connecting center of dodecahedron with center of pentagon will give normal vector. – BlacKow Jun 03 '15 at 02:56
  • Now that I think about it, it might be a bit easier to just compute the barycenter of a face, shift the face so that the barycenter is at the origin, perform your pentagram transformation, and then shift back to the original position. (For the barycenter, use averagepoints[], which is also in the link I previously gave. – J. M.'s missing motivation Jun 03 '15 at 02:57
  • But the face will still be tilted (not parallel to coordinate plane), what's the point of shifting it? – BlacKow Jun 03 '15 at 03:04
  • Why, did you already try applying your pentagram[] to a tilted but shifted pentagon? – J. M.'s missing motivation Jun 03 '15 at 03:14
  • @Guesswhoitis. The shift doesn't seem to work because all calculations are exact, so shifting a face back and forth gives the same values for vertex coordinates. The problem occurs during rendering. – BlacKow Jun 03 '15 at 17:50
  • I see the same bug in V9.0.1. – Michael E2 Aug 02 '15 at 00:07

1 Answers1

9

A shot in the dark: Reverse the orientation. Hey, it works...but I don't know why...???

Graphics3D[Polygon /@ Reverse@*pentagram /@ (vert[[#]] & /@ ind)]

Mathematica graphics

A guess at what's happening. I'm not sure of the reason why things work correctly when one coordinate is the same for all vertices and do not work when the plane of the polygon is oblique. In the oblique case, the triangulation consists of triangles all based at the first vertex in the polygon. This works when a polygon is convex, but not always for a star.

MeshCells[
 DiscretizeGraphics@ Graphics3D@ Polygon@ pentagram@ vert[[First[ind]]], 2]
(*
  {Polygon[{1, 9, 10}], Polygon[{3, 1, 2}], Polygon[{4, 1, 3}], Polygon[{5, 1, 4}],
   Polygon[{6, 1, 5}], Polygon[{7, 1, 6}], Polygon[{8, 1, 7}], Polygon[{9, 1, 8}]}
*)

The cell indices are the same if Reverse@ is inserted before pentagram.

So when the polygon's vertex list start with a vertex at a convex corner, artifacts are produced; when it starts with a concave corner, the polygon is drawn correctly -- except, as I said, when one coordinate is the same for all vertices.

The behavior can be reproduced in the triangulation algorithm of DiscretizeGraphics:

Graphics3D[{Polygon[#], 
    MapIndexed[Text[Style[#2, "Label", Bold, 16], #1] &, #]} &@
  RotateLeft@pentagram@vert[[First[ind]]]
 ]

DiscretizeGraphics@ Graphics3D@ Polygon@ pentagram@ vert[[First[ind]]]
DiscretizeGraphics@ Graphics3D@ Polygon@ Reverse@ pentagram@ vert[[First[ind]]]

Mathematica graphics Mathematica graphics Mathematica graphics

Reversing the order puts vertex 10 first in the list. We can also rotate the list so that an concave corner starts the list.

Graphics3D[{Polygon[#], 
    MapIndexed[Text[Style[#2, "Label", Bold, 16], #1] &, #]} &@
  RotateLeft@ pentagram@ vert[[First[ind]]]
 ]

Mathematica graphics

Michael E2
  • 235,386
  • 17
  • 334
  • 747