Find all "chains" in the poset of divisors

Question

I want to input a set of divisors of an integer $n$ and return all subsets of these divisors ${d_1,d_2,...d_k=n}$ such that $d_1$ divides $d_2$, $d_2$ divides $d_3$, ... and $d_(k-1)$ divides $d_k$. I would like to have a code that could be understood by a beginner Mathematica user.

As a possible starting point: Select[Subsets[Divisors[n], {3, DivisorSigma[0, n]}], And @@ (Divisible @@@ Partition[Reverse[#], 2, 1]) &]; doing this in a more efficient manner is something I'll leave for people smarter than me to do… ;) — J. M.'s missing motivation, Jun 03 '15 at 13:38
Re: I would like to have a code that could be understood by a beginning Mathematica user.. Code is just code, and can be understood by anyone furnished with suitable documentation, the appropriate behavioral drivers and some time to spare. Sometimes it can be understood by language interpreters too. — Dr. belisarius, Jun 04 '15 at 00:48
@Guess who it is, Thanks. Your code was very helpful. I learned a lot! — Geoffrey Critzer, Jun 04 '15 at 15:06
@Belisarius, Thanks for your comment. Here is what happens when a beginning Mathematica user has lots of time to spare:Table[Timing[ Table[Length[ Select[Subsets[Divisors[n], {k}], Apply[And, Map[Apply[Divisible, #] &, Partition[Reverse[#], 2, 1]]] &]], {k, 1, PrimeOmega[n] + 1}]], {n, Table[Apply[Times, Prime[Range[m]]], {m, 0, 5}]}] ... and we are led to Sloane's OEIS A038719 — Geoffrey Critzer, Jun 04 '15 at 15:08
@GeoffreyCritzer Nice!. This is the equivalent expression using my answer Join @@ (Join[{DivisorSigma[0, #]}, Tally[Length /@ allChains[#]][[All, 2]]] & /@ Table[Times @@ Prime[Range[m]], {m, 1, 7}]) .But I think it's slower! — Dr. belisarius, Jun 04 '15 at 16:12
@GeoffreyCritzer well, I performed the timed tests wrong. Mine is actually much, much faster — Dr. belisarius, Jun 04 '15 at 19:37
Compare Timing[Join @@ Table[Table[ Length[Select[Subsets[Divisors[n], {k}], Apply[And, Map[Apply[Divisible, #] &, Partition[Reverse[#], 2, 1]]] &]], {k, 1, PrimeOmega[n] + 1}], {n, Table[Apply[Times, Prime[Range[m]]], {m, 0, 5}]}]] — Dr. belisarius, Jun 04 '15 at 19:39
with Timing[Join @@ (Join[{DivisorSigma[0, #]}, Tally[Length /@ allChains[#]][[All, 2]]] & /@ Table[Times @@ Prime[Range[m]], {m, 1, 5}])] — Dr. belisarius, Jun 04 '15 at 19:39

score 11 · Accepted Answer · edited Apr 13 '17 at 12:55

A graph representation:

opts = {VertexLabels -> "Name", ImagePadding -> 10};

g[n_] := Graph[Flatten[Thread[DirectedEdge[#, Most@Divisors@#]] & /@ Divisors@n], opts]

aa = g[30]

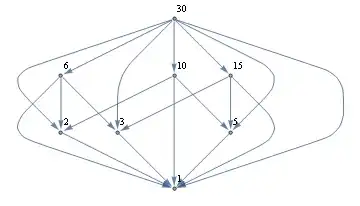
Mathematica graphics

Then (v10 only, thanks to @billc for running it for me):

fp = FindPath[aa, 30, 1, Infinity, All]
(*
 {{30, 1}, {30, 15, 1}, {30, 10, 1}, {30, 6, 1}, {30, 5, 1}, 
  {30, 3, 1}, {30, 2, 1}, {30, 15, 5, 1}, {30, 15, 3, 1}, {30, 10, 5, 1}, 
  {30, 10, 2, 1}, {30, 6, 3, 1}, {30, 6, 2, 1}}
*)

(For pre-v10 options see here)

Now, all the adjacent sublists in those lists are valid chains.

Union @@ (Flatten[Table[#[[i ;; j]], {j, 2, Length@#}, {i, 1, j - 1}], 1] & /@ fp)

(*
 {{2, 1}, {3, 1}, {5, 1}, {6, 1}, {6, 2}, {6, 3}, {10, 1}, {10, 2}, 
  {10, 5}, {15, 1}, {15, 3}, {15, 5}, {30, 1}, {30, 2}, {30, 3}, {30, 5}, 
  {30, 6}, {30, 10}, {30, 15}, {6, 2, 1}, {6, 3, 1}, {10, 2, 1}, {10, 5, 1},
  {15, 3, 1}, {15, 5, 1}, {30, 2, 1}, {30, 3, 1}, {30, 5, 1}, {30, 6, 1},
  {30, 6, 2}, {30, 6, 3}, {30, 10, 1}, {30, 10, 2}, {30, 10, 5}, {30, 15, 1},
  {30, 15, 3}, {30, 15, 5}, {30, 6, 2, 1}, {30, 6, 3, 1}, {30, 10, 2, 1}, 
  {30, 10, 5, 1}, {30, 15, 3, 1}, {30, 15, 5, 1}}
*)

The last step is also equivalent to:

Union@Flatten[ReplaceList[#, {___, i_, x___, j_, ___} :> {i, x, j}] & /@ fp, 1]

Finally, the whole thing can be packed up in a function like:

allChains[n_] := Module[{a, fp},
  a = Graph@ Flatten[Thread[DirectedEdge[#, Most@Divisors@#]] & /@ Divisors@n];
  fp = FindPath[a, n, 1, Infinity, All];
  Union @@ (Flatten[Table[#[[i ;; j]], {j, 2, Length@#}, {i, 1, j - 1}], 1] & /@ fp)
  ]

Looks great! I think your use of an abundant number is a good example… — J. M.'s missing motivation, Jun 03 '15 at 23:07
@J. M. Glad you like it. I enjoy a lot this kind of solutions, trying to convert a problem into some area where Mma is strong. — Dr. belisarius, Jun 03 '15 at 23:26

Find all "chains" in the poset of divisors

1 Answers1