Here is what I have done thus far:
h = x^2 - y^2 + z;
g = z;
Manipulate[
ContourPlot3D[{h == 0, g == k}, {x, -3, 3}, {y, -4, 4}, {z, -2, 2},
MeshFunctions -> {Function[{x, y, z}, h - g]},
MeshStyle -> {{Thick, Blue}},
Mesh -> {{0}},
ContourStyle ->
Directive[Orange, Opacity[0.8], Specularity[White, 30]]],
{{k, 0}, -2, 2, Appearance -> "Labeled"}]
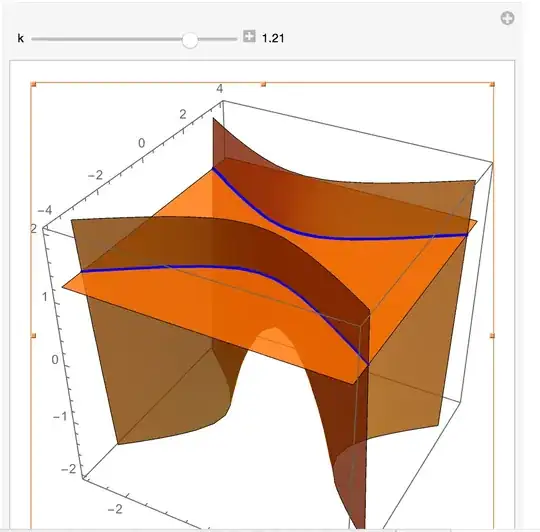
And the resulting image:

Clearly, I am doing something wrong? Any suggestions?
Update: I should have put Mesh->{{k}}.
h = x^2 - y^2 + z;
g = z;
Manipulate[
ContourPlot3D[{h == 0, g == k}, {x, -3, 3}, {y, -4, 4}, {z, -2, 2},
MeshFunctions -> {Function[{x, y, z}, g - h]},
MeshStyle -> {{Thick, Blue}},
Mesh -> {{k}},
ContourStyle ->
Directive[Orange, Opacity[0.8], Specularity[White, 30]]],
{{k, 0}, -2, 2, Appearance -> "Labeled"}]
Which works.
Mesh -> None, BoundaryStyle -> {{1, 2} -> {Thick, Blue}}? – kglr Jun 03 '15 at 19:30Mesh -> {{k}}, MeshFunctions -> {Function[{x, y, z}, z]}? – Basheer Algohi Jun 03 '15 at 19:46{1,2}mean in{{1, 2} -> {Thick, Blue}}? – David Jun 03 '15 at 21:41(5968); uses the same trick, but still guler can provide more info. – Sektor Jun 03 '15 at 21:52BoundaryStyleis undocumented. I must have learnt it from Daniel's answer in the link given by @Sektor.{1,2}means the "boundary" between surfaces1and2. – kglr Jun 05 '15 at 21:17