VoronoiMesh without edges

Question

How can I remove the edges of a VoronoiMesh? I would like to display only the closed cells not touching the border of the image.

This is my binarized source image (imgbw):

enter image description here

I am doing this:

comp = SelectComponents[imgbw, "Area", # > 10 &]; 
meanValues = ComponentMeasurements[MaxDetect[DistanceTransform[comp]], 
           "Centroid"];
listData = meanValues /. Rule -> List;
listData = listData[[All, 2]];
vm = VoronoiMesh[listData];
Show[imgbw, HighlightMesh[vm, Style[1, Black]], ImageSize -> 720]

The output is:

enter image description here

score 14 · Answer 1 · answered Jun 09 '15 at 19:10

14

Shorter, though undocumented:

Graphics[{LightBlue, EdgeForm[Black], 
    MeshPrimitives[vm, {2, "Interior"}]}, ImageSize -> 720]

enter image description here

answered Jun 09 '15 at 19:10

ilian

25,474
4
117
186

+1 for playing with tricks where others have to do the dirty work. Are there other specifiers like "Interior" that one should know about? – halirutan Jun 10 '15 at 01:20
Great. From where did you get this undocumented info? – mrz Jun 10 '15 at 09:58
2

@Milenko Let's just say it is a perk of the job. – ilian Jun 10 '15 at 16:21
@ilian: Ah, now I understand everything ... I clicked at your name - great that you are helping us. I was last week in Frankfurt and met some developers and also Conrad ...It was more than great to listen to their presentations and to talk to them – mrz Jun 11 '15 at 08:31
I think the "InteriorFaces" can work too.You can get it by vm[pts]["Properties"],But I don't know how to do it. – yode Feb 22 '17 at 12:54

RunnyKine · Accepted Answer · 2015-06-15T01:31:39.547

EDIT

New Answer

Using the RegionBounds and IntersectingQ functions we can easily achieve this. First we collect the cells of the Voronoi diagram and compute their region bounds, then comparing with that of the overall Voronoi diagram we can select the interior polygons.

(* vm is the Voronoi diagram of your image *)

cells = MeshPrimitives[vm, 2]; (* cells of the Voronoi diagram *)
regb = RegionBounds[vm]; (* region bounds of the Voronoi diagram *)
inout = IntersectingQ[Flatten@regb, Flatten@RegionBounds[#]] & /@ cells;
in = Pick[cells, inout, False]; (* select the inner polygons *)

Here is the plot:

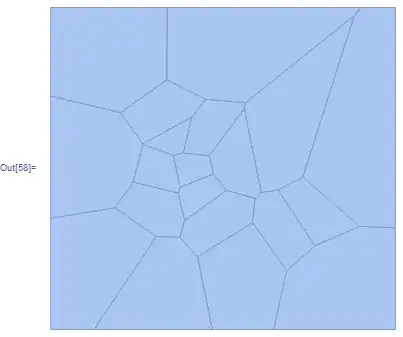
Graphics[{Blue, EdgeForm[Black], in}]

Mathematica graphics

Old Answer

Here is one approach:

I will use my sample data here, see below for your image data.

pts = RandomReal[4, {20, 2}];
vor = VoronoiMesh[pts]

Mathematica graphics

We determine the boundary points using RegionBoundary and we set the points from the Voronoi diagram that are on the boundar to {0,0}. We do this so we can eliminate the Polygons that coincide with the boundary (this is your goal).

nobdr = With[{bdr = MeshCoordinates@RegionBoundary@vor, 
              cod = MeshCoordinates[vor]}, 
             If[MemberQ[bdr, #], {0, 0}, #] & /@ cod]

We now get the positions of those boundary points

ind = Position[nobdr, {0,0}] // Flatten;

And delete the polygons as explained above:

pol = DeleteCases[MeshCells[vor, 2], 
  Polygon[{___, Alternatives @@ ind, ___}]]

Now the images:

gr = Graphics[{LightRed, EdgeForm[Black], GraphicsComplex[nobdr, pol]}]

Mathematica graphics

With the Voronoi diagram

Show[vor, gr]]

Mathematica graphics

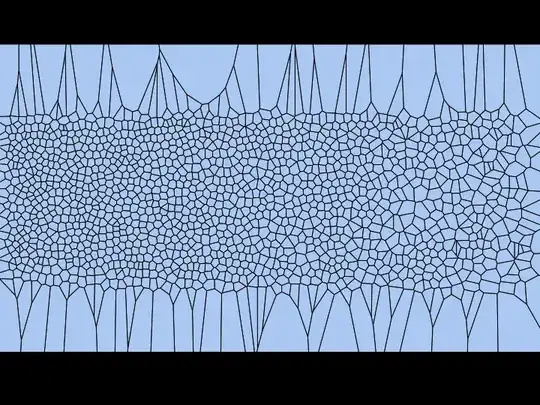
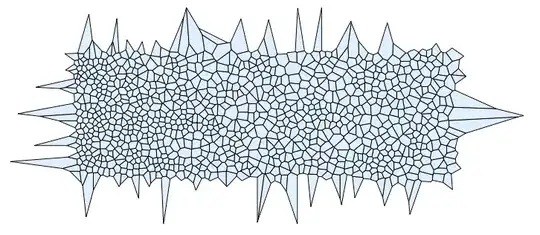
The same approach applied to your data gives:

Mathematica graphics

In the future, you can get the image by copying the URL and doing something likeimgbw = Import["http://i.stack.imgur.com/yvNQS.png"]. — 2012rcampion, Jun 09 '15 at 15:41
Can you comment on what you are doing with Sow with one argument in your If statement? I'm curious because I don't see any corresponding Reap. — dionys, Jun 09 '15 at 19:55
@dionys Please ignore the Sow that was a left-over from a previous try. — RunnyKine, Jun 09 '15 at 20:04

VoronoiMesh without edges

2 Answers2

Linked