I have a dataset of which I'm attempting to determine the full width at half maximum. A picture of the data is given below, and the dataset itself can be found here (pastebin). 
Now, this set has a minimum, which can be found rather easily. Say we call the data yy, then by using Min[yy] we've found the minimum. To find the full width half max, it is then probably easiest to look for a point closest to 1-(1-Min[yy])*0.5 in yy. The first thing that came to mind was using Nearest[yy,1-(1-Min[yy])*0.5,1] which indeed returns a value of yyclosest to half of the FWHM. But I'm having some trouble finding the actual position of this point in the data. Ironically, using Position[yy,Nearest[yy,1-(1-Min[yy])*0.5,1]] seems to come up empty. I'm not sure why exactly this is, but maybe there is some rounding going on, or incompatible outputs. I've tried thinking of a solution to this, but it doesn't seem obvious to me.
My question is therefore if anyone seems a workaround, or an all around better idea. My plan was to find this position of the half-max point, find the corresponding xx, subtract the xx element of the position of the max, and multiply by two. I don't need a 100% perfect estimation; this should be good enough.
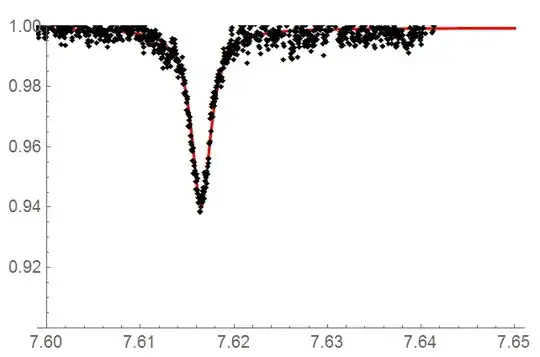 The fit (visually is not unreasonable, adjusted $R^2$ 0.999989).
The fit (visually is not unreasonable, adjusted $R^2$ 0.999989). 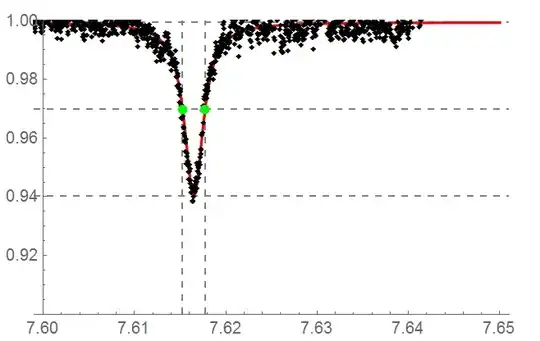
nf = Nearest[Table[ps[[i]] -> i, {i, Length[ps]}]] (* so it returns the index of the site *)which is exactly what I needed to get Nearest working in my function. – user129412 Jun 15 '15 at 00:09