How to draw a protractor in Mathematica

Question

I would like to draw a protractor with Mathematica. I hope this is a fun question. Here is some start codes I tried:

r1 = 0.95; r2 = 0.98; r3 = 0.9; R = 1;
Show[{ParametricPlot[{{Cos[x], Sin[x]}, {2 x/Pi - 1, 0}}, {x, 0, Pi}, 
   PlotStyle -> Black], 
  Table[ParametricPlot[{{Cos[i Degree] x, x Sin[i Degree]}}, {x, r2, 
     R}, PlotRange -> {-R, R}], {i, 0, 180}], 
  Table[ParametricPlot[{{Cos[i Degree] x, x Sin[i Degree]}}, {x, r1, 
     R}, PlotRange -> {-R, R}], {i, 0, 180, 5}], 
  Table[ParametricPlot[{{Cos[i Degree] x, x Sin[i Degree]}}, {x, r3, 
     R}, PlotRange -> {-R, R}], {i, 0, 180, 10}]}, Axes -> False]

start figure

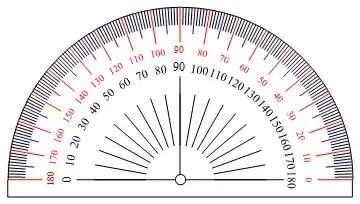
I draw this protractor just for fun. I hope someone may be interested in this question. As advice from @shrx, the skeleton of the protractor is drawn. However, the labels are not easy for me to add, the alignment and direction are not easy task to do. Any suggestion on this part?

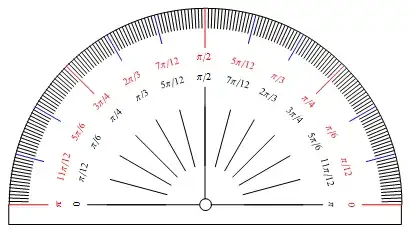
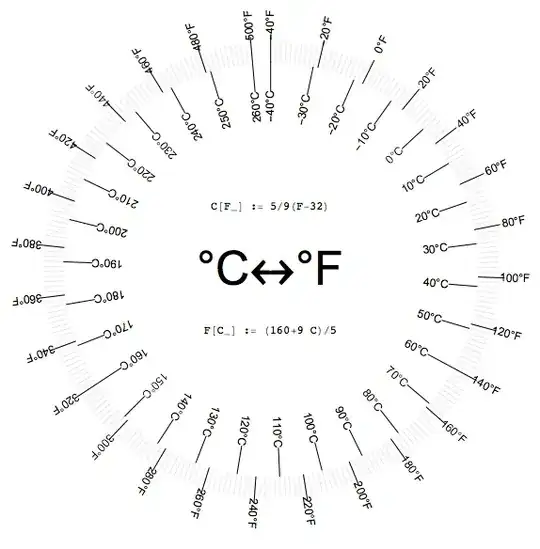
Here are some protractor designs from wiki:

wiki

wiki 1

Thanks for @george2079's answer

The correct way to draw this kind object is directly draw each part, not as in the question using parametric equations to draw. I slightly modified @george2079's answer based on @wxffles's suggestion.

Graphics[{{Thickness[.003], Circle[{0, 0}, 1, {0, Pi}], 
   Circle[{0, 0}, .03], 
   Line[{{1, 0}, {1, -.1}, {-1, -.1}, {-1, 0}}]},
  {Thickness[.001], Line[{{-0.015, 0}, {0.015, 0}}], 
   Line[{{0, -0.015}, {0, 0.015}}]},
  Rotate[{Thickness[.003], Line[{{.03, 0}, {.6, 0}}]}, #, {0, 
      0}] & /@ {0, Pi/2, Pi},
  GeometricTransformation[
     Piecewise[{{{Red, Line[{{.8, 0}, {1, 0}}], Black, 
         Line[{{.2, 0}, {.5, 0}}], 
         Rotate[{Red, 
           Text[Style[#, FontSize -> Scaled[0.028], 
             FontFamily -> "Times"], {.75, 0}, {0, 0}]}, -Pi/2], 
         Rotate[{Black, 
           Text[Style[180 - #, FontSize -> Scaled[0.026], 
             FontFamily -> "Times"], {.65, 0}, {0, 0}]}, -Pi/2]}, 
        Mod[#, 10] == 0}, {{Blue, Line[{{.85, 0}, {1, 0}}]}, 
        Mod[#, 5] == 0}, {Line[{{.9, 0}, {1, 0}}], True}}], 
     RotationTransform[# Degree]] & /@ (Range[0, 180])}]

from answer

Thank you all for your answers and comments!

Please edit your post in the form of a question. Right now it is unclear what you're asking. You have clearly managed to draw a protractor, it's just missing some finishing details. — shrx, Jun 16 '15 at 13:49
@shrx texts alignment and direction are quite tough question for me. — Kattern, Jun 16 '15 at 14:02
Related to your text rotation issue http://mathematica.stackexchange.com/q/5719/193 — Dr. belisarius, Jun 16 '15 at 14:30

george2079 · Accepted Answer · 2015-06-17T14:47:27.570

Graphics[{Circle[{0, 0}, 1, {0, Pi}], Circle[{0, 0}, .03], 
     Line[{{1, 0}, {1, -.1}, {-1, -.1}, {-1, 0}}],
     Rotate[ Line[{{.03, 0}, {.6, 0}}] , #, {0, 0}] & /@ {0, Pi/2, Pi},
  GeometricTransformation[
     Piecewise[{
       {{Red, Line[{{.8, 0}, {1, 0}}], Black, 
         Line[{{.2, 0}, {.5, 0}}], 
          Rotate[{Red, Text[#, {.75, 0}, {0, 0}]}, -Pi/2], 
          Rotate[{Black, 
             Text[Style[180 - #, Larger], {.65, 0}, {0, 0}]}, -Pi/2]}, 
            Mod[#, 10] == 0},
       {{Blue, Line[{{.85, 0}, {1, 0}}]}, 
            Mod[#, 5] == 0},
       {Line[{{.9, 0}, {1, 0}}], True}}], 
           RotationTransform[# Degree]] & /@ (Range[0, 180])}]

enter image description here

the mathematicians version...

formpi[v_] := Module[ { frac = v/Pi,num,den },
   num = If[Numerator[frac] == 1, Unevaluated[Sequence[]], 
                                  Numerator[frac]];
   den = If[Denominator[frac] == 1, Unevaluated[Sequence[]],
               {"/", Denominator[frac]}];
   Switch[
     frac, 1, Pi , 0, 0,
         x_Integer, Row[{frac, Pi}],
         x_Rational, Row[{num, Pi}~Join~den], __, Row[ {v/Pi, Pi}  ] ]]
  Graphics[{Circle[{0, 0}, 1, {0, Pi}], Circle[{0, 0}, .03], 
  Line[{{1, 0}, {1, -.1}, {-1, -.1}, {-1, 0}}], 
  Rotate[Line[{{.03, 0}, {.6, 0}}], #, {0, 0}] & /@ {0, Pi/2, Pi}, 
  GeometricTransformation[Piecewise[{
    {{Red, Line[{{.8, 0}, {1, 0}}], Black, 
      Line[{{.2, 0}, {.5, 0}}], 
       Rotate[{Red, Text[Style[formpi[#]], {.75, 0}, {0, 0}]}, -Pi/2],
       Rotate[{Black, 
       Text[Style[formpi[Pi - #]], {.65, 0}, {0, 0}]}, -Pi/2]}, 
         Mod[#, Pi/4 ] == 0},
     {{Blue, Line[{{.85, 0}, {1, 0}}], Black, 
             Line[{{.2, 0}, {.5, 0}}], 
           Rotate[{Red, Text[Style[formpi[#]], {.75, 0}, {0, 0}]}, -Pi/2],
        Rotate[{Black, 
            Text[Style[formpi[Pi - #]], {.65, 0}, {0, 0}]}, -Pi/2]}, 
          Mod[#, Pi/12] == 0}, {Line[{{.9, 0}, {1, 0}}], True}}], 
       RotationTransform[# ]] & /@ (Range[0, Pi  , Pi/180])}]

enter image description here

May I suggest using a relative font size? Instead of something like Style[#, Larger], I like to use Style[#, FontSize->Scaled[0.02]. It makes it easier when resizing and exporting graphics. — wxffles, Jun 16 '15 at 22:47
Very nice - I feel like a cro-magnon cave artist when I see results like this, +1 — ciao, Jun 17 '15 at 06:33
@wxffles good point, I didn't realize you could do specify a Scaled FontSize. — george2079, Jun 17 '15 at 14:27

score 10 · Answer 2 · answered Jun 16 '15 at 20:18

This is not a protractor, but it is a related application that that serves as an example of rotated text which is the only thing missing in the protractor shown in the question.

I did it a while a go and keep it near the kitchen oven:

c[f_]:=5/9 (-32+f)

f[c_]:=1/5 (160+9 c)

cToAngle[c_]:=(c+40)/300*(2\[Pi]-5Degree)

fToAngle[f_]:=(f+40)/540*(2\[Pi]-5Degree)

Module[{k1=0.86,k2=1.128},
  Graphics[
    {Style[Text["\[Degree]C\[LeftRightArrow]\[Degree]F",{0,0}],FontSize->50],
     Style[Text["C[F_] := 5/9(F-32)",{0,.3}],FontFamily->"Courier"],
     Style[Text["F[C_] := (160+9 C)/5",{0,-.3}],FontFamily->"Courier"],
     Table[{Line[{k1{Sin[cToAngle@c],Cos[cToAngle@c]},{Sin[cToAngle@c],Cos[cToAngle@c]}}],
            Text[ToString[c]<>"\[Degree]C",k1{Sin[cToAngle@c],Cos[cToAngle@c]},{1,0},{Sin[cToAngle@c],Cos[cToAngle@c]}]},
           {c,-40,260,10}],
     Table[{Line[{{Sin[fToAngle@f],Cos[fToAngle@f]},k2*{Sin[fToAngle@f],Cos[fToAngle@f]}}],
            Text[ToString[f]<>"\[Degree]F",(k2+0.125){Sin[fToAngle@f],Cos[fToAngle@f]},{1,0},{Sin[fToAngle@f],Cos[fToAngle@f]}]},
           {f,-40,500,20}],
     AbsoluteThickness[0.1],
     Table[{Line[{{Sin[fToAngle@f],Cos[fToAngle@f]},(1.1)*{Sin[fToAngle@f],Cos[fToAngle@f]}}]},
           {f,-40,500,2}],
     White,Point[{0,0}]},BaseStyle->{FontSize->Larger}
  ]
]

enter image description here

This doesn't make a good protractor because this circle weirdly has 540 degrees, and not 360 ;-P
+1 — evanb, Jun 17 '15 at 15:47

How to draw a protractor in Mathematica

Thanks for @george2079's answer

2 Answers2

Linked