Solving differential equation but keeping showing running

Question

I am trying to solve this differential equation, see the command below. But the cell keeps showing that it is running without giving any answer for a very long time. Eventually I had to abort it. Does anybody know what I did wrong?

Clear[y];

DSolve[{(4*y[x] - 1 - 4 x - 6 x^2) (x^2 y'[x] + (1 - x) y[x]) == 
   3*y[x] (1 + 3 x (1 + 2 x + 2 (x^2))), y[0] == 1}, y[x], x];

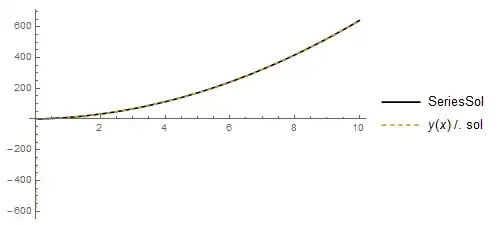
Use NDSolve, and to avoid problems at x == 0 don't include this point in the range of integration — e.g. put your initial condition at x = 0.001. — Stephen Luttrell, Jun 17 '15 at 08:32

score 4 · Answer 1 · edited Apr 13 '17 at 12:55

At x = 0 we have a singular point. Calculation of analytical solutions will take eternity.

sol = NDSolve[{(4*y[x] - 1 - 4 x - 
6 x^2) (x^2 y'[x] + (1 - x) y[x]) == 
3*y[x] (1 + 3 x (1 + 2 x + 2 (x^2))), y[0.00001] == 1}, 
y[x], {x, 0, 10}] // Quiet;

Plot[y[x] /. sol, {x, 0, 10}]

enter image description here

If we want to express solution using Taylor Series:

initconds = {y[0] == 1};
odeOperator = (-4 - 12 x - 20 x^2 - 12 x^3) # + (4 - 
   4 x) #^2 + (-x^2 - 4 x^3 - 6 x^4 + 4 x^2 #) D[#, x] &;
xx = Series[y[x], {x, 0, 10}];
soln = SolveAlways[Join[{odeOperator[xx] == 0}, initconds], x];
SeriesSol = Normal[xx /. soln[[1]]];

Plot[{SeriesSol, y[x] /. sol}, {x, 0, 10}, 
PlotLegends -> "Expressions", PlotStyle -> {Black, Dashed}]

enter image description here

Solving differential equation but keeping showing running

1 Answers1