The following is (I believe) a better implementation for at least two reasons. First, it doesn't use the old Splines package, but Interpolation[..., Method -> "Spline"] instead. Second, if uses an algorithmic arc length parametrization to get the equispaced points instead of relying on the mesh generated by ParametricPlot which is nice for displaying but not designed for extracting the points' coordinates from the plot.
I also modified the way you are measuring the inter-monomer angles, for the better, I think.
ClearAll[setMonomerPoints, getInterpolatingCurve,
getEquispacedPointsOnCurve, arcLenReparametrization];
setMonomerPoints[numberOfMonomers_, monomerLength_, angleSigma_] :=
Module[{angles, anglePath},
anglePath[angles_, a_] := FoldList[#+ a {Cos@#2,Sin@#2} &, {0,0}, Accumulate@angles];
angles = RandomVariate[NormalDistribution[0, angleSigma], numberOfMonomers];
anglePath[angles, monomerLength]
]
getInterpolatingCurve[pts_, interpOrder_] := Module[{prepList},
prepList = MapIndexed[{#2[[1]], #1} &, pts];
Interpolation[prepList, Method -> "Spline", InterpolationOrder -> interpOrder]
]
getEquispacedPointsOnCurve[fun_InterpolatingFunction, numberOfpoints_] :=
Module[{cLen, dom = First@fun["Domain"], z, arcLenReparametrization,
eqNewCoords, eqParmRange},
arcLenReparametrization[f_, len_] := arcLenReparametrization[f, len] =
Module[{t, s}, NDSolveValue[{t'[s] == 1/Norm[f'[t[s]]], t[0] == dom[[1]]},
t, {s, 0, len}]];
(* Calculate total curve arc length *)
cLen = NIntegrate[Norm[fun'[z]], Evaluate@{z, Sequence @@ dom}, MaxRecursion -> 12];
(* generate numberOfpoints+1 points along the interval {0, cLen} *)
eqParmRange = Rescale[Range[0, 1, 1/numberOfpoints], {0, 1}, {0, cLen}];
(* Calculate the value of the function's parameter in those points *)
eqNewCoords = arcLenReparametrization[fun, cLen][eqParmRange];
(* calculate the position for the equispced points *)
fun /@ eqNewCoords]
A test drive:
SeedRandom[42];
nMonomers = 80;
ss = setMonomerPoints[nMonomers, 1, .2];
f = getInterpolatingCurve[ss, 3];
eqsp = getEquispacedPointsOnCurve[f, nMonomers];
ListPlot[{ss, eqsp}, AspectRatio -> Automatic,
PlotStyle -> {{PointSize[.01], Green}, {PointSize[.005], Black}}]

The points look the same because the curve is smooth but it "follows" the segmented line quite well. But despite the look, they aren't the same:
ListPlot[EuclideanDistance @@@ Transpose[{ss, eqsp}]]
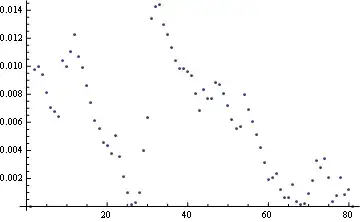
Please note that if you change in the code above
eqsp = getEquispacedPointsOnCurve[f, nMonomers];
by
eqsp = getEquispacedPointsOnCurve[f, nMonomers / 2];
You'll get:

Let's generate and check the angle's statistic you're worried about. We will use the Cross product instead of VectorAngle to preserve the signs:
SeedRandom[42];
nMonomers = 80;
sigma = .2;
p1 = Table[setMonomerPoints[nMonomers, 1, sigma], {100}];
p2 = getEquispacedPointsOnCurve[#, nMonomers] & /@ (getInterpolatingCurve[#, 3] & /@ p1);
vecc2 = Partition[#, 2, 1] & /@ Differences /@ p2;
vecc3 = vecc2 /. {x : _?NumericQ, y_?NumericQ} :> {x, y, 0};
angc = ArcSin[Flatten[Map[Cross @@ #/Times @@ Norm /@ # &, vecc3, {2}][[All, All, 3]]]];
GraphicsRow[{Histogram[angc, {.01}],
ProbabilityPlot[angc, NormalDistribution[0, sigma]]}]
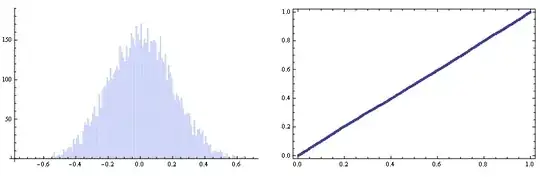 So everything looks fine enough :)
So everything looks fine enough :)
Finally a warning note: If you have a good fit for the interpolating curve but you can't estimate well the number of monomers, the statistics may go astray. Just look;
SeedRandom[42];
nMonomers = 80;
sigma = .2;
p1 = Table[setMonomerPoints[nMonomers, 1, sigma], {100}];
(* Note the "2" in the line below *)
p2 = getEquispacedPointsOnCurve[#, nMonomers/2] & /@ (getInterpolatingCurve[#, 3]&/@ p1);
vecc2 = Partition[#, 2, 1] & /@ Differences /@ p2;
vecc3 = vecc2 /. {x : _?NumericQ, y_?NumericQ} :> {x, y, 0};
angc = ArcSin[Flatten[Map[Cross @@ #/Times @@ Norm /@ # &, vecc3, {2}][[All, All, 3]]]];
GraphicsRow[{Histogram[angc, {.01}],
ProbabilityPlot[angc, NormalDistribution[0, sigma]]}]
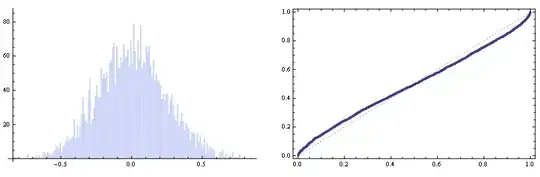



 So everything looks fine enough :)
So everything looks fine enough :)
ListPlot[coord[[1]]]and I got plots that looked good. UsingListPlotit was looking good before sorting and I guess it was so because it was just showing me the coordinates. When I used,ListPlotwith lines option it wasn't good at all. Is there a sequential way of extracting the co-ordinates? Even though thep1is in sequential the angles calculated from it does not have the same distribution asangles– sra Jun 19 '15 at 16:23SplineFitis introducing some artifact of not. By testingSplineFiton artificially created polymer ( of which I know almost everything about (e.g. arc length, persistence length)), I can be sure about robustness ofSplineFitand then I can use it on some experimental data. When I tried to useSplineFiton my experimental data I was getting some weird answer. – sra Jun 19 '15 at 16:31Part::partd: "Part specification cc[[{9,3,4,5,46,75,30,6,35,67,50,39,17,36,68,64,12,57,29,47,18,13}]] is longer than depth of object."when I triedcoord = Table[ cc[[First@ FindCurvePath[ cc = Cases[Normal@plot[[i]], Point[p_] :> p, Infinity]]]] , {i, num}];– sra Jun 19 '15 at 16:33