0
r[t_] = Piecewise[{{{7 t, 0, 4 (1 + Cos[ t])}, 
     0 <= t <= π}, {{5 Cos[t - 3 π/2] + 7*π, 
      3 Sin[t - 3 π/2] + 3, 0}, π < t <= 
      2 π}, {{7*π + 3*Cos[t - 3 π/2], 
      2*3 - 3 + 3*Sin[t - 3 π/2], 2/(3 π) (t - 2 π)^2}, 
     2 π < t <= 4 π}, {{7 π - 5 (t - 4 π), 
      6 + 4 ((t - 4 π)/π)^3, 
      2 - 1/π t^2 + 10 t - 22 π}, 
     4 π < t <= 5 π}, {{-3 t + 17 π, 10, 
      2 - 972 π + 540 t - (99 t^2)/π + (6 t^3)/π^2}, 
     5 π < t <= 6 π}, {{-π - 3 Sin[t], 
      9/40 (1/3 (20 + 18 π) - t)^2, 3 Cos[t] - 1}, 
     6 π < t <= 
      8 π}, {{-25 π + 25 t - (19 t^2)/(4 π) + t^3/(
       4 π^2), -(25/2) (140 - 132 π + 27 π^2) + (
       15 (80 - 74 π + 15 π^2) t)/(2 π) - (
       3 (180 - 164 π + 33 π^2) t^2)/(
       8 π^2) - ((-50 + 45 π - 9 π^2) t^3)/(20 π^3), 
      1058 - (360 t)/π + (81 t^2)/(2 π^2) - (3 t^3)/(
       2 π^3)}, 8 π < t <= 10 π}}];

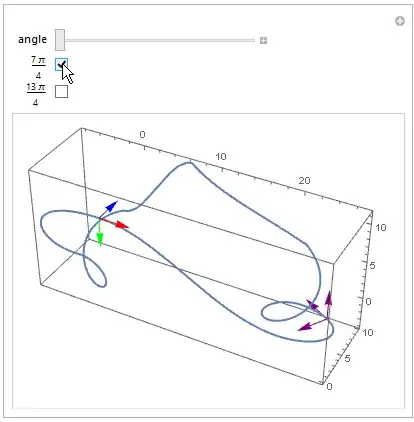
I have no idea how to put the vectors on the curve, im not sure even if i calculated the right vectors. I found a similar question on this site and used the method I found there, but now im stuck on plotting the vectors. Any help will be greatly appreciated.

Here is the code I used to get the three vectors as well.

uT[t_] := Simplify[r'[t]/Norm[r'[t]], t ∈ Reals]
vN[t_] := Simplify[uT'[t]/Norm[uT'[t]], t ∈ Reals]
vB[t_] := Simplify[Cross[r'[t], r''[t]]/Norm[Cross[r'[t], r''[t]]], t ∈ Reals]

I want to place such vectors at t = 7π/2 and t = 13π/2

m_goldberg
  • 107,779
  • 16
  • 103
  • 257
Odom Seng
  • 1
  • But you've read this already, right? – J. M.'s missing motivation Jun 19 '15 at 19:15
  • Welcome to Mathematica.SE! I hope you will become a regular contributor. To get started, 1) take the introductory Tour now, 2) when you see good questions and answers, vote them up by clicking the gray triangles, because the credibility of the system is based on the reputation gained by users sharing their knowledge, 3) remember to accept the answer, if any, that solves your problem, by clicking the checkmark sign, and 4) give help too, by answering questions in your areas of expertise. – bbgodfrey Jun 19 '15 at 19:20
  • @Guesswhoitis. I posted an answer as the OP uses the functions (copy and pasted) from the links suggested by you and Jens...this piecewise function, I think posed some challenges so I posted. – ubpdqn Jun 20 '15 at 07:35

1 Answers1

1

The link in the comment is excellent. To plot TNB frame to a point you need to a line/arrow from point ($\vec{r}(t)$ to relevant vector, e.g. $\vec{r}(t)+\vec{T}(t)$.

There are some indeterminate points (at piecewise junctions but the desired points are well defined). Just for illustration:

tang[t_] := r'[t]/Sqrt[r'[t].r'[t]]
norm[t_] := tang'[t]/Sqrt[tang'[t].tang'[t]]
bin[t_] := Cross[tang[t], norm[t]]
arr[t_] := Arrow[{r[t], r[t] + 4 #}] & /@ Through[{tang, norm, bin}[t]]

Visualizing:

Manipulate[
 Show[ParametricPlot3D[r[t], {t, 0, 10 Pi}], 
  Graphics3D[{Riffle[{Red, Green, Blue}, arr[angle
      ]], {Purple, If[p1 == 1, arr[7 Pi/4], Sequence[]], Pink, Thick, 
     If[p2 == 1, arr[13 Pi/4], Sequence[]]}}]], {angle, 0.01, 
  10 Pi - 0.01}, {{p1, 0, 7 Pi/4}, {0, 1}, 
  Checkbox}, {{p2, 0, 13 Pi/4}, {0, 1}, Checkbox}]

enter image description here

Notes: (i) the reason I redefined the tangent, norm and binormal was due to problems with Norm... (ii) the FrenetSerretSystem had problems with this piecewise function but I have used for simpler functions

ubpdqn
  • 60,617
  • 3
  • 59
  • 148