4

I want to smooth a unit step function for use in NDSolve so this function is a smooth function of time (t). How can I do the smoothing? The unit step function is defined by:

α = π/6;
Vbusd[t_] := 5 (1 - Exp[-t]);
Vbusq[t_] := 3 Exp[-t];

n = UnitStep[Vbusd[t]*Cos[t - α - π/6] - Vbusq[t]*Sin[t - α - π/6]]  -
    UnitStep[Vbusd[t]*Cos[t - α - (5 π)/6] - Vbusq[t]*Sin[t - α - (5 π)/6]];
m_goldberg
  • 107,779
  • 16
  • 103
  • 257
mard
  • 41
  • 3
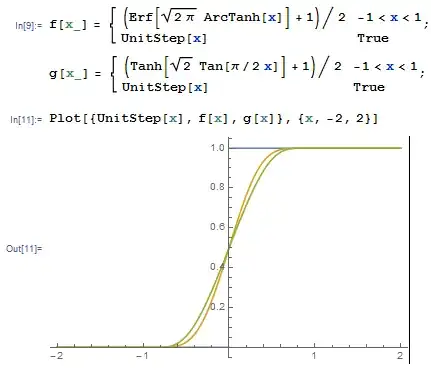
  • After a second look I think your question is a little unclear. What do you really want? Smoothen n with NDSolve or find a smooth approximation of n which is to be used in NDSolve? – xzczd Jun 21 '15 at 09:17
  • Thanks alot for help. finding a smooth approximation of n which is to be used in NDSolve. – mard Jun 21 '15 at 09:21
  • 1
    I normally use Tanh – yohbs Jun 21 '15 at 10:48

1 Answers1

4

These are the transitions I usually use: (both are $C^{\infty}$)

f[x_] = Piecewise[{{(Erf[Sqrt[2 π] ArcTanh[x]] + 1)/2, -1 < x < 1}}, UnitStep[x]]
g[x_] = Piecewise[{{(Tanh[Sqrt[2] Tan[π/2 x]] + 1)/2, -1 < x < 1}}, UnitStep[x]]

Plot[{UnitStep[x], f[x], g[x]}, {x, -2, 2}]

Picture

Sektor
  • 3,320
  • 7
  • 27
  • 36
Coolwater
  • 20,257
  • 3
  • 35
  • 64
  • 1
    Could you please post text (code-styled markdown) that can be cut and pasted rather than images of your code? This makes it easy for people to grab your solution and experiment with it. – dionys Jun 21 '15 at 12:45
  • 1
    But I do not know time of rising and falling levels for difinition of unitstep and Tanh ! – mard Jun 21 '15 at 13:24