4

Consider a list like below:

ttable={{0, 2.6596 - 66.137 I}, {1/9, 2.45339 - 65.3148 I}, {2/9, 
  1.82053 - 62.8922 I}, {1/3, 0.720006 - 58.9982 I}, {4/
  9, -0.911205 - 53.8382 I}, {5/9, -3.15056 - 47.6797 I}, {2/
  3, -6.08057 - 40.8346 I}, {7/9, -9.77826 - 33.6382 I}, {8/
  9, -14.3047 - 26.4282 I}, {1, -19.6947 - 19.5216 I}}`

by defining "f" as interpolating function we'll have:

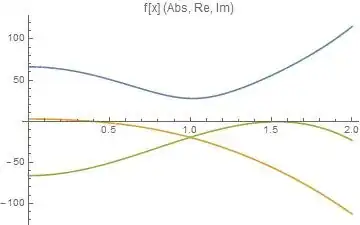
f = Interpolation[ttable]

now we define ff as the following integration:

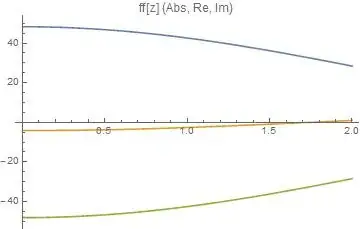
ff[\[Xi]_]:=NIntegrate[(f[rr]) Cos[rr \[Xi]], {rr, 0, 1}]

the first problem is that this function can not be calculated and I have no idea why the followoing error happens:

In[87]:= ff[.1]
During evaluation of In[87]:= NIntegrate::inumr: The integrand Cos[rr \[Xi]] InterpolatingFunction[{{0.,1.}},{4,15,0,{10},{4},0,0,0,0,Automatic,{},{},False},<<1>>,{
Developer`PackedArrayForm,{0,<<10>>},{2.6596 -66.137 I,<<8>>,-19.6947-19.5216 I}},{Automatic}][rr] has evaluated to non-numerical values for all sampling points in the region with boundaries {{0,0.111111}}. >>
Out[87]= NIntegrate[f[rr] Cos[rr \[Xi]],{rr,0,1}]

The other thing should be mentioned is that I have to use ff in integrand of another integration like below: 

NIntegrate[ff[\[Xi]] * \[Xi],{\[Xi],0,3}]

I've manipulated the former equations in many ways but none of them made an accurate output for the last integration, so I would be greatly thankful if somebody out there could help me!

zag
  • 45
  • 3
  • Works like a charm for me on Mathematica 10.1 running on MacOS 10.10.3, just had to remove the apostrophe in the definition of ttable, which is probably a typo anyways. – Wizard Jun 23 '15 at 10:10
  • @Wizard the ff function sometimes works and sometimes not which makes me really confused but what about the last integral could you calculate it too?! cause that one never showed to be solved!!! – zag Jun 23 '15 at 10:21
  • about that apostrophe, yes that was a typo! and I'm using mathematica 10.0 running on windows 8 if it helps in any aspects! – zag Jun 23 '15 at 10:25
  • Can't reproduce your problem. ff[.1] evaluates to -4.1238 - 48.0535 I in V10.1 running on OS X (10.10.2). – m_goldberg Jun 23 '15 at 11:06
  • 1
    I'm voting to close this question as off-topic because the problem the user claims to be experiencing can not be reproduced. – m_goldberg Jun 23 '15 at 11:08
  • @m_goldberg Dear sir could you calculate NIntegrate[ff[\[Xi]] * \[Xi],{\[Xi],0,3}] too?!!!! – zag Jun 23 '15 at 11:15
  • 2
    @m_goldberg I got the same error as posted by the OP, so I'm voting to leave this question open. – Sjoerd C. de Vries Jun 23 '15 at 12:50

3 Answers3

6

The most important information is that you used your function ff inside another NIntegrate, because this is the source of confusion. What you have to know is that NIntegrate doesn't start right away with the numerical calculation when you call

NIntegrate[ff[ξ]*ξ, {ξ, 0, 3}]

It will try to do some analysis of your integrand and most likely, it will try to evaluate ff[ξ] without putting in numbers. And what happens then? Right, you call the NIntegrate of ff without proper numerical value of ξ:

Mathematica graphics

The solution is pretty simple: Change your definition of ff so that it only calls its NIntegrate body when the argument is indeed numeric:

ClearAll[ff];
ff[ξ_?NumericQ] := NIntegrate[(f[rr]) Cos[rr ξ], {rr, 0, 1}]
NIntegrate[ff[ξ]*ξ, {ξ, 0, 3}]

(* 4.28747 - 124.522 I *)
halirutan
  • 112,764
  • 7
  • 263
  • 474
  • Sometimes I feel there should be a wrapper to perform this NumericQ trick automatically... and probably it's completely feasible(?) – kirma Jun 23 '15 at 12:02
  • @kirma, In V10.1 (OSX), I get the messages but the NIntegrate goes through and gets the right answer. As you point out, the warnings are coming from the inside NIntegrate, but the outside NIntegrate seems not to care much. One could view this as a compromise position, allowing the computation but warning the user in case it's a mistake. – Michael E2 Jul 01 '15 at 23:48
4

Everthing woks out fine (in version 10 at least) if you take care of a consistent name of the integration variable.

Let's repeat all steps

1) Table of data

In[1]:= ttable = {{0, 2.6596 - 66.137 I}, {1/9, 2.45339 - 65.3148 I}, {2/9, 
   1.82053 - 62.8922 I}, {1/3, 
   0.720006 - 58.9982 I}, {4/9, -0.911205 - 53.8382 I}, {5/9, -3.15056 - 
    47.6797 I}, {2/3, -6.08057 - 40.8346 I}, {7/9, -9.77826 - 33.6382 I}, {8/9, -14.3047 - 26.4282 I}, {1, -19.6947 - 19.5216 I}};

2) Interpolation

In[2]:= f = Interpolation[ttable]
(* output skipped here *)

Check some values

f[#] & /@ {0, 1/2, 2/3, 1}

(*
Out[27]= {2.6596 - 66.137 I, -1.94971 - 50.8643 I, -6.08057 - 40.8346 I, -19.6947 - 19.5216 I}
*)

Plot real quantities derived from f

Plot[{Abs[f[x]], Re[f[x]], Im[f[x]]}, {x, 0, 2}, 
 PlotLabel -> "f[x] (Abs, Re, Im)"]
(* 150623_plot_f.jpg *)

enter image description here

3) Define ff

Clear[ff]

ff[z_] := NIntegrate[f[x] Cos[x z], {x, 0, 1}]

Plot the function ff

Plot[{Abs[ff[z]], Re[ff[z]], Im[ff[z]]}, {z, 0, 2}, 
 PlotLabel -> "ff[z] (Abs, Re, Im)"]
(* 150623_plot_ff.jpg *)

enter image description here

4) Finally define f1 as the definite numerical integral over ff

f1[y_] := NIntegrate[ff[x], {x, 0, y}]

f1[1.]

(* Out[39]= -2.94907 - 45.2287 I *)

No problem. So it seems. But if you would have chosen in the definition of f1 another name of the integration variable (x) than the name of the integration variable in the definition of ff then an error would appear. It sounds funny, but try it, take t instaed.

Dr. Wolfgang Hintze
  • 13,039
  • 17
  • 47
  • I'm probably going nuts here but for me it makes a difference whether I write NIntegrate[ff[x], {x, 0, 1}] which works fine, or whether I use NIntegrate[ff[z], {z, 0, 1}], which gives a different result and throws errors. – halirutan Jun 23 '15 at 12:08
  • And btw it seems your solution works fine because you used x and not ξ like OP did. Really weird – halirutan Jun 23 '15 at 12:12
  • @ halirutan : 1) That is why I posted my answer. And, BTW, I was not telling WHY things are as they are but just how to solve the problem. 2) I could have as well used xi instead of y in the definition of ff. But I prefer latin letters in order to make the Mathematica text easier legible. – Dr. Wolfgang Hintze Jun 23 '15 at 12:34
  • 1
    @halirutan NIntegrate[ff[x], {x, 0, 1}] yields the same errors for me as xi did. – Sjoerd C. de Vries Jun 23 '15 at 12:54
  • My results are for "10.1.0 for Microsoft Windows (64-bit) (March 24, 2015)". The integration which led to errors in your cases is that of my parapraph 4. – Dr. Wolfgang Hintze Jun 23 '15 at 16:23
1

This is not an answer but rather a comment/example on @Dr.WolfgangHintze and @halirutan posts, concerning the "weird" behaviour that was observed with NIntegrate, that is localization and symbolic evaluation of the variables which may actually lead to unwanted results:

Edit

I'll take an even more simple example which concerns both NIntegrate and Integrate:

fNI[a_] := NIntegrate[a*hello, {hello, 0, 1}]
fI[a_]  :=  Integrate[a*hello, {hello, 0, 1}]

then ok:

fNI[1]
fI[1]

0.5
1/2

but

fNI[hello]
fI[hello]

0.333333
1/3

I would expect it to be rather 0.5 hello and 1/2 hello ?!

Previous

I'll take a very simple example:

Let's define:

f[a_] :=           NIntegrate[a*hello, {hello, 0, 1}]
fN[a_?NumericQ] := NIntegrate[a*hello, {hello, 0, 1}]

Would you expect:

NIntegrate[f[hello], {hello, 0, 1}]

0.333333

which corresponds actually to NIntegrate[NIntegrate[hello*hello, {hello, 0, 1}], {hello, 0, 1}] !!!

whereas

NIntegrate[f[x], {x, 0, 1}]

enter image description here

0.25

and

NIntegrate[fN[x], {x, 0, 1}]

0.25

and

NIntegrate[fN[hello], {hello, 0, 1}]

0.25

SquareOne
  • 7,575
  • 1
  • 15
  • 34
  • 1
    Note that NIntegrate[f[hello], {hello, 1, 2}] also gives 0.333333: the outer integration range does not matter! – Alexey Popkov Jul 02 '15 at 02:36
  • @AlexeyPopkov Actually, replacing NIntegrate by Integrate shows that : Integrate[f[hello], {hello, a, b}] returns 0.333333 (-a + b) – SquareOne Jul 02 '15 at 10:04
  • It isn't surprising because Integrate does not have a Hold* attribute and f[hello] is evaluated before Integrate. So actually Integrate[f[hello], {hello, a, b}] is equivalent to Integrate[0.333333, {hello, a, b}]. – Alexey Popkov Jul 02 '15 at 10:43
  • @AlexeyPopkov Actually i did not try to simply evaluate f[hello] ! See my edit. – SquareOne Jul 02 '15 at 11:58
  • All your observations are the expected and well-documented behavior (while may be not immediately obvious). For me the interesting observation was only the nested NIntegrate case which is identical to the nested Block case: citing the Documentation, "NIntegrate effectively uses Block to localize variables." The f[hello] case is just how the lexical scoping works. – Alexey Popkov Jul 02 '15 at 12:14