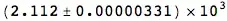Tidy form of numbers with errors using ScientificForm

Question

Say I've computed something and got a number 0.02112398 with a computed error: 0.000331 Formatting it with ScientificForm[0.02112398 \[PlusMinus] 0.000331] gives me: $$ 2.1124 \times 10^{-2} \pm 3.31 \times 10^{-4} $$

How can I make it display it like this instead? (notice common exponent and the same number of digits)

$$ (2.1124 \pm 0.0331) \times 10^{-2} $$ having the option to cut some digits in both numbers would be a nice addition, for example displaying it like this: $$ (2.11 \pm 0.03) \times 10^{-2} $$

Related: "Expression of uncertainty in measurement.", "Formatting a number with fixed number of significant digits." — Alexey Popkov, Jul 02 '15 at 20:33

Karsten7 · Accepted Answer · 2015-07-02T09:40:42.627

9

PlusMinus[{x_, err_}] := 
 Module[{errE = Last@MantissaExponent[err], xE = Last@MantissaExponent[x]}, 
  Row[{"(", 
    NumberForm[N@Round[x, 10^(errE - 1)]*10^(-xE + 1), {xE - errE + 1, xE - errE}], 
    " \[PlusMinus] ", 
    NumberForm[N@Round[err, 10^(errE - 1)]*10^(-xE + 1), {1, xE - errE}, 
     ExponentFunction -> (Null &)], ")", 
    " \[Times] ", 
    DisplayForm@SuperscriptBox["10", ToString[xE - 1]]}]]
PlusMinus[x_, err_] := PlusMinus[{x, err}]

Now

PlusMinus@{0.02112398, 0.000331}

or

0.02112398 ± 0.000331

and after the last edit also

PlusMinus@{0.02112398, 0.0000000000331}

edited Jul 02 '15 at 09:40

answered Jul 02 '15 at 01:30

Karsten7

27,448
5
73
134

1

PlusMinus@{0.02112398, 0.000331} works well, but PlusMinus@{0.2112398, 0.00331} does not. – bbgodfrey Jul 02 '15 at 04:22
@bbgodfrey Thanks for pointing that out. Should be fixed now. – Karsten7 Jul 02 '15 at 09:41

score 6 · Answer 2 · edited Jun 16 '20 at 09:23

6

Here is my take on this problem.

errorForm[num_, err_, digits_] :=
 Module[{exp, n, e},
  exp = Floor @ Log10 @ num;
  n = NumberForm[num/10^exp, digits, ExponentFunction -> (Null &)];
  e = NumberForm[err/10^exp, digits, ExponentFunction -> (Null &)];
  Row[{
    "(", n, "\[ThinSpace]\[PlusMinus]\[ThinSpace]", e, ")
    \[ThinSpace]\[Times]\[ThinSpace]", Superscript["10", exp]}]]
errorForm[2.1124^-2, 3.31^-4, 3]

(2.11\[ThinSpace]\[PlusMinus]\[ThinSpace]0.0331)\[ThinSpace]*\[ThinSpace]10^-2

which looks this

formatting

in a Mathematica notebook.

Update

I have edited my function to deal with the issue raised by Mr.Wizard. Now

 errorForm[2.1124*^3, 3.31*^-3, 4]

produces

formated

edited Jun 16 '20 at 09:23

Community

1

answered Jul 02 '15 at 06:49

m_goldberg

107,779
16
103
257

1

@Mr.Wizard. I think I have fixed it. – m_goldberg Jul 02 '15 at 12:09
I copied your answer into a Mathematica code block and then converted it to Input style, as you kindly suggested in Meta1493, and it introduced \n between the second and third lines of Row. Great answer in any case (+1). – bbgodfrey Jul 02 '15 at 13:33
@bbgodfrey. Yes, that is an artifact of copy and paste. The code as written in the original notebook doesn't have the problem. If I removed the line break between the last two lines of the Module above, copy and paste would work fine, but the answer would be harder to read. What to do? :-) – m_goldberg Jul 02 '15 at 15:09
You can copy the Row code in Unicode format, and it fits on one line. Although \[ThinSpace] then disappears from sight, it still is there and works when the code is copied back to Mathematica. I tried it to be sure. – bbgodfrey Jul 02 '15 at 15:12
@bbgodfrey. But I really, really want readers to be able see all the special characters needed to get the formatting to look right. I think that's a very important feature of the answer. – m_goldberg Jul 02 '15 at 15:16
You can (just barely) make it fit by replacing all but \[ThinSpace] by Unicode and replacing "10" by 10: "(", n, "\[ThinSpace]±\[ThinSpace]", e, ")\[ThinSpace]×\[ThinSpace]", Superscript[10, exp] with the opening Row[{ and closing }]. on the preceding and following lines. – bbgodfrey Jul 02 '15 at 15:34

score 5 · Answer 3 · answered Jul 02 '15 at 11:45

5

Likely some duplication with existing answers but I felt like playing with this one. I'll use Format so that the underlying representation does not change.

a_ ± b_ ± c_ := PlusMinus[a, b, c];

Format[b_?NumericQ ± err_?NumericQ ± acc_Integer: 6] ^:=
  Row[{
    "(",
     NumberForm[Row[{b, err}*10^-#, "±"], {acc, acc}, 
      ExponentFunction -> (Null &)],
    ")",
    Superscript["×\[ThinSpace]10", #]
  }] & @ ⌊Log10 @ Abs @ b⌋

Now with the default six digits of accuracy:

-0.02112398 ± 3.31*^-8

(-2.112400 ± 0.000003) × 10^-2

Or only three:

-0.02112398 ± 3.31*^-8 ± 3

(-2.110 ± 0.000) × 10^-2

The FullForm of the last expression:

% // FullForm

PlusMinus[-0.02112398`, 3.31`*^-8, 3]

This means that you can easily extract values or overload operations for PlusMinus as needed.

answered Jul 02 '15 at 11:45

Mr.Wizard

271,378
34
587
1,371

Great answer (+1), but it spills over into other open notebooks, even when they have different default contexts. How can this prevented? Also, could you add more explanation to your answer? – bbgodfrey Jul 02 '15 at 12:16
1

@bbgodfrey (1) This is defined upon a System` operator so it is global. One could use a head besides PlusMinus at the expense of the pretty entry form. (2) I would be happy to but what would you like explained? – Mr.Wizard Jul 02 '15 at 12:22
I am trying to understand the first line of your answer. For instance, in a new notebook, i_ ± j_ := i + 1 works, but i_ := i + 1 does not. – bbgodfrey Jul 02 '15 at 12:42
2

@bbgodfrey The PlusMinus operator is left-associative, therefore a ± b ± c is parsed as PlusMinus[PlusMinus[a, b], c] but I want to use and make a definition for the three parameter form PlusMinus[a, b, c]. The definition a_ ± b_ ± c_ := PlusMinus[a, b, c]; converts the former into the latter. A definition requires an active head to attach the rule to; in i_ ± j_ := i + 1 that head is PlusMinus; in i_ := i + 1 you have a bare Pattern which is not something you can attach a rule to. – Mr.Wizard Jul 02 '15 at 12:54
(+1) Notes: 1) Probably it is better to not show the exponent when it is zero; 2) You should apply N to {b, err} in order to work with _?NumericQ correctly (Integer, Rational etc.). – Alexey Popkov Jul 02 '15 at 20:06
@Alexey Thanks! I'll see what I can do about that tomorrow. – Mr.Wizard Jul 03 '15 at 00:35

bbgodfrey · Answer 4 · 2015-07-02T12:00:09.897

2

This seems to be close to what is wanted.

a1 = 0.02112398; a2 = 0.000331;
f[z1_, z2_] := Module[{t, ee = Floor[Log10[Abs[z1]]]}, 
                  t = NumberForm[z1 10^-ee, 3] ± NumberForm[z2 10^-ee, 3 + ee, 
                  ExponentFunction -> (Null &)]; t RawBoxes[SuperscriptBox[10, ee]]]
f[a1, a2]

$$ (2.11 \pm 0.03) 10^{-2} $$

edited Jul 02 '15 at 12:00

answered Jul 02 '15 at 01:28

bbgodfrey

61,439
17
89
156

1

@Mr.Wizard Now fixed. Thanks. – bbgodfrey Jul 02 '15 at 12:00

score 0 · Answer 5 · answered Jul 02 '15 at 01:37

Ugly, but seems close to what you seek:

myTidyForm[a_Real, b_Real] := (
   {"(" ~~ ToString[#[[1, 1]]] ~~ "\[PlusMinus]" ~~ 
       ToString[#[[2, 1]] 10^(#[[2, 2]] - #[[1, 2]])] ~~ ")\[Times]" ~~
        ToString[10]^ToString[#[[1, 2]]]} &@(MantissaExponent /@ {a, 
       b}))[[1]]

Tidy form of numbers with errors using ScientificForm

5 Answers5

Update