Multiplying three matrices does not give expected form

Question

I'm having lectures on analytic geometry. I've learned that there is an associated matrix multiplication for a quadratic form:

$\quad \quad \left( \begin{array}{ccc} x & y & 1 \\ \end{array} \right) \left( \begin{array}{ccc} a & \frac{b}{2} & \frac{d}{2} \\ \frac{b}{2} & c & \frac{e}{2} \\ \frac{d}{2} & \frac{e}{2} & f \\ \end{array} \right) \left( \begin{array}{c} x \\ y \\ 1 \\ \end{array} \right)$

When I try to make Mathematica compute that, it says that objects of unequal length can't be combined. But I have no idea of why that happens, I mean I assume that Mathematica may expect some other way to perform the matrix multiplication of this. But I don't know how it should be done.

The code is as follows:

( {
   {x, y, 1}
  } )* ( {
   {a, b/2, d/2},
   {b/2, c, e/2},
   {d/2, e/2, f}
  } )*( {
   {x},
   {y},
   {1}
  } )

You need to post Mathematica code, not LaTeX. Otherwise it's impossible to tell what's going wrong. Also be sure to type "matrix multiplication" in the documentation search box and see what comes up. — Szabolcs, Jul 02 '15 at 09:02
@Szabolcs But I just typed in with Mathematica palletes: http://i.imgur.com/mtEIUI2.png — Red Banana, Jul 02 '15 at 09:04
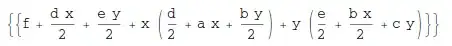
The problem is that * is element by element multiplication and only works for arrays of the same dimensions. . (i.e. Dot) is used for matrix multiplication. Using $1\times n$ and $n\times 1 $ matrices for row and column vectors is not a problem, but not necessary either. For a vector you can just write {x,y,z} and not distinguish between row and column vectors. The order of multiplications (vec.mat vs mat.vec) determines what will be done. — Szabolcs, Jul 02 '15 at 09:05
One needs to be careful when just typing classical mathematical notation into Mathematica. Sometimes Mathematica can interpret it, sometimes it can't. When it can, it might not use the interpretation you meant. It's better to treat any Mathematica input as program code, not human-readabale mathematical notation, and use unambiguous notations. The palettes are for mathematica notation mostly. But in this case the only change necessary is . really, the matrix notation is not harmful in any way. — Szabolcs, Jul 02 '15 at 09:08
Yes, it's a generalized scalar product that works between arrays/tensors of any dimension, not just matrices. For matrices it's equivalent to matrix multiplication. Contrast this with e.g. MATLAB, which originally supported only matrices and nothing else. MATLAB still doesn't support vectors (1D arrays), only row-matrices or column-matrices. Mathematica does have true 1D arrays and doesn't have the strict matrix-oriented view that MATLAB takes. — Szabolcs, Jul 02 '15 at 09:10
For a more extended discussion on column and row vectors see this. — Sjoerd C. de Vries, Jul 02 '15 at 11:58

score 4 · Answer 1 · answered Jul 02 '15 at 09:05

Matrices (and also vectors and other tensors) are multipled using Dot.

Using your code, just replace * by . (I also removed all ('s and )'s as they don't do anything in this context.

{{x, y, 1}}.{{a, b/2, d/2}, {b/2, c, e/2}, {d/2, e/2, f}}.{{x}, {y}, {1}}

Result:

enter image description here

Multiplying three matrices does not give expected form

1 Answers1