5

I am using NDSolver and WhenEvent to solve a system of differential equations. I get this message:

NDSolve::ndsz: At t == 49169.954923435114`, step size is effectively zero; singularity or stiff system suspected.

The solution I get is pretty stable until that time, then blows off completely. At each evaluation I get the same behaviour at different times.

I understand that the problem might lie with the fact that I am solving for very long times, and eventually the algorithm just starts having problems handling all the data.

Is there a way to stop the solver as soon as the error comes up?

Andrea
  • 558
  • 2
  • 14
  • 1
    Doesn't the solver already stop exactly at the point mentioned? – J. M.'s missing motivation Jul 04 '15 at 10:52
  • Maybe it does, but the solution is then just extrapolated for the remaining time. Is there a way to return the last time t before the error? I am thinking of something like WhenEvent["error", tfinal = t] – Andrea Jul 04 '15 at 11:29
  • Maybe this http://mathematica.stackexchange.com/questions/66590/breaking-out-of-ndsolve?rq=1 – Mariusz Iwaniuk Jul 04 '15 at 13:13
  • Unfortunately the system does not hit a singularity, so I have no way to analytically identify a point where to stop the integration, like in the link. There is no way to make it stop in response to the error itself? – Andrea Jul 04 '15 at 13:28
  • 3
    Let's say you have sol = NDSolve[..., x, {t, 0, 100000}]. The x["Domain"] /. sol will yield {{{0, 49169.954923435114}}}, and you can get the time it stopped. You can also use the option NDSolve[..., "ExtrapolationHandler" -> {Indeterminate&}] and the solution won't extrapolate; however, it will return Indeterminate, which may be good or may cause other problems. Without explicit code, we're just guessing. – Michael E2 Jul 04 '15 at 17:43
  • Usually, the solution already has gone bad before this error occurs. Try plotting your solution near where NDSolve failed. – bbgodfrey Jul 05 '15 at 01:12
  • @MichaelE2, the "x["Domain"] /. sol" method works perfectly for me. If you write it up as an answer I can accept it. – Andrea Jul 05 '15 at 13:49
  • @bbgodfrey in the body of my question it says explicitly that the solution is well behaved until the time of the error. I suspect the error comes from rounding errors as the system is an ODE but the singularity is hit at different times at each run. – Andrea Jul 05 '15 at 13:49
  • @AndreaDiBiagio The OP of (48556) also had a problem with round-off error and NDSolve::ndsz. – Michael E2 Jul 05 '15 at 17:46

1 Answers1

6

First, a test case:

sol = NDSolve[{x'[t] == -1/x[t], x[0] == -1}, x, {t, 0, 2}]

NDSolve::ndsz: At t == 0.499999735845871`, step size is effectively zero; singularity or stiff system suspected. >>

Mathematica graphics

Consult What's inside InterpolatingFunction[{{1., 4.}}, <>]? or InterpolatingFunctionAnatomy and you will discover that InterpolatingFunction comes with lots of utilities and methods that give access to a wealth of information. In particular, the method "Domain" will yield the domain of the InterpolatingFunction, which in this case will be the interval over which NDSolve successfully integrated the ODE (up to the point where stiffness stopped it). 

{tstart, tstop} = Flatten[x["Domain"] /. sol]
(*  {0.`, 0.499999735845871`}  *)

A couple of ways to plot. Note for ListLinePlot, you don't need to know the domain; it and ListPlot handle InterpolatingFunction as a special case.

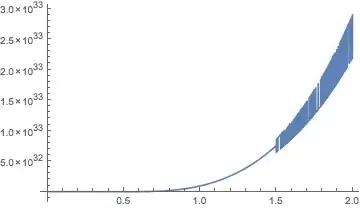
ListLinePlot[x /. sol]
Plot @@ {{x[t], x'[t]} /. First[sol], Flatten@{t, x["Domain"] /. sol}}

Mathematica graphics

By default, going past the ends of the domain results in extrapolation.

Plot[x[t] /. First[sol], {t, 0, 2}]

Mathematica graphics

One can use the option, mentioned in a comment in the linked question, "ExtrapolationHandler" to override the default extrapolation.

sol2 = NDSolve[{x'[t] == -1/x[t], x[0] == -1}, x, {t, 0, 10}, 
   "ExtrapolationHandler" -> {Indeterminate &}];

Plot[x[t] /. First[sol2], {t, 0, 2}]

NDSolve::ndsz: At t == 0.4999997164125506`....

Mathematica graphics

Community
  • 1
Michael E2
  • 235,386
  • 17
  • 334
  • 747