How to apply stress (moment) graph color to cylindrical surface?

Question

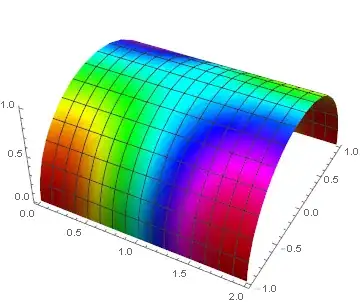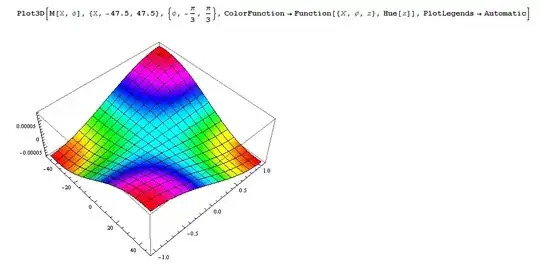
enter image description here

so i want to apply this graph colors to cylindrical surface.

enter image description here

Thanks Ahead!

Code:

l = 95
P = 270000
R = 15.8
h = 1.1
K = 2.9*10^10
a = 30.1
b = 1
c = Pi/2
d = 1/15.8
M[X_, ϕ_] := (-((12*P*R^4)/(K*h^3)))*
  Sum[(((4/(Pi*m))*Sin[((m*Pi)/l)*a]*Sin[((m*Pi)/l)*b]*(4/(Pi*n))*
        Sin[((n*Pi)/((2/3)*Pi))*c]*

        Sin[((n*Pi)/((2/3)*Pi))*
          d])/(((n/((2/3)*Pi))*Pi)^8 - ((n/((2/3)*Pi))*
           Pi)^6 + ((12*R^6)/h^2)*((m/l)*Pi)^4))*
         Sin[((m*Pi)/l)*X]*Sin[((n*Pi)/((2/3)*Pi))*ϕ], {m, 1, 
    5}, {n, 1, 5}]

Plot3D[M[X, ϕ], {X, -47.5, 47.5}, {ϕ, -(π/3), π/3}, 
 ColorFunction -> Function[{X, ϕ, z}, Hue[z]], 
 PlotLegends -> Automatic]

Please post copyable code instead of pictures. That will increase the probability that someone tries to answer your question. We hate unnecessary typing. — Sjoerd C. de Vries, Jul 08 '15 at 17:17
Hello, thanks for reply and suggestions. I am new at this site and to mathematica. I tried to post copyable code instead of picture but i did not figure out how to do it. when i copyed my code it appeared as strange symbols. Could you please help me? Should i make new post or it is possible to edit this one? — John, Jul 08 '15 at 21:10
Have a look at this meta question for copying and this one for getting Greek symbols etc. displayed as such. — Sjoerd C. de Vries, Jul 08 '15 at 21:31
Thanks a lot I will read it and improve my post. Could you please help me meanwhile with this one? Day after tomorrow I have presentation and that's why i am hurrying. — John, Jul 08 '15 at 21:35
You really have to paste the code here. The picture has m's and n's that are virtually indistinguishable and the same for 1's and l's (el). I cannot reproduce your figure at all. — Sjoerd C. de Vries, Jul 08 '15 at 22:21
https://www.dropbox.com/s/ewqreq78bnazuh7/Untitled-2%20W%20axali.nb?dl=0 here I have uploaded mathematica file. Please do not think that I am lazy and I am not pasting code on purpose: I have tryed it and read you links but still doing something wrong and need time to get used to that. — John, Jul 08 '15 at 23:13
by the way in file is given graph for radial displacements for cylindrical shell. now i want to insert cylindric shell with same parameters (length =95m; and arc = 2pi/3 radian) and apply graph colors.Your help will be great favor me. — John, Jul 08 '15 at 23:19
@John I copied what seemed to be the relevant parts of your code to your post. Check that I've done what you would have wanted. All I did before copying was to select the cell and execute the menu command Cell > Convert To > InputForm. Clarification of what you're asking is better made by editing the post, not through comments. I'm not sure what you mean by "arc = 2pi/3" when you show 1/2 a cylinder. — Michael E2, Jul 09 '15 at 04:19
The pasted code differs significantly from the code in the picture... — Sjoerd C. de Vries, Jul 09 '15 at 05:29
One can probably adapt my answer to Better way to visualize cylinder puzzle solution to this task. — Jens, Jul 09 '15 at 05:39
Thank you guys for all your friendly responses and not insulting newbie. With the time I will try to get more familiar to the mathematica and site and to improve my posts. — John, Jul 09 '15 at 10:34

score 4 · Accepted Answer · edited Feb 04 '17 at 11:35

I created a cylinder using ParametricPlot3D and used your function as the ColorFunction.

I set the X coordinate to the range 0-2 and scaled it as the input to your function by 47.5*X-47.5.

I had to scale your function M[X,ϕ] by dividing it by its approximate range (0.00016) and adding 0.5 before using it as an input to Hue.

I am not convinced that the solution is correct but at least it points you in the general direction of how to plot a surface and use another function as the ColorFunction.

ParametricPlot3D[
 {X, Sin[3 ϕ/2], Cos[3 ϕ/2]},
 {X, 0, 2},
 {ϕ, -π/3, π/3},
 Boxed -> False,
 Axes -> True,
 ColorFunction ->
  Function[{x, y, z, X, ϕ},
   Hue[0.5 + M[47.5 X - 47.5, ϕ]/0.00016]
   ],
 ColorFunctionScaling -> False
 ]

Mathematica graphics

You are Brilliant! thanks a lot! That's exactly what I was asking. It was great help to me. — John, Jul 09 '15 at 10:22

How to apply stress (moment) graph color to cylindrical surface?

1 Answers1