I have an interplanetary trajectory simulation that calculates the required velocity (using a Lambert solver) and escape angle for a spacecraft to travel from Earth to Mars. This model does not use a patched conic approximation (where trajectory segments are "patched" together), but instead uses a fully integrated approach where the gravitational attraction of the Earth, Mars and Sun all act on the spacecraft concurrently at any given time in the simulation. As such, the spacecraft's escape angle from low-Earth orbit (which is calculated using patched-conic equations) is not accurate enough to produce a trajectory that will hit Mars directly, and is usually off by quite a lot (about 10%-20%) due to the pull of Earth's gravitational field when the spacecraft leaves Earth.
Thus, what I've tried to do is use ParametricNDSolve and NMinimize to perform numerical optimization and scan through a parameter p that acts as an escape angle "correction coefficient". The optimizer scans through values of p until it finds the desired value of p that will correct the Earth ejection angle and give an accurate trajectory that reaches Mars at a predefined periapse radius (which is 300km above Mars' surface in this case as shown in the code below).
Below is a stripped down version (it excludes the Lambert solver and various other calculations that do not need to be shown) of the simulation code that shows the optimization process:
Remove["Global`*"]
(*Gravitational Constant*)
G = 6.672*10^-11;
(*Simulation running time, in seconds (1 day = 86400 seconds)*)
tmax = (1000) (86400);
(*Spacecraft time-of-flight between Earth and Mars, in seconds (1 day = 86400 seconds)*)
TOF = (254) (86400);
(*Mass of Sun, Earth, Mars (from JPL's Horizons ephemeris), in kilograms*)
ms = 1.988544*10^30 ;(*Mass of Sun*)
me = 5.97219*10^24 ;(*Mass of Earth*)
mm = 6.4185*10^23 ;(*Mass of Mars*)
(*Planetary radii of Sun, Earth and Mars (from JPL's Horizons ephemeris), in metres*)
r[0] = 6.963*10^8 ;(*Mean radius of Sun*)
r[1] = 6.37101 *10^6;(*Mean radius of Earth*)
r[2] = 3.3899*10^6 ;(*Mean radius of Mars*)
(*Heliocentric positions of Earth and Mars (from JPL's Horizons ephemeris) on 26 November 2011, in metres*)
pe = 149597870700 {4.416639858432274*10^-1, 8.798967504313304*10^-1} ;
pm = 149597870700 {-8.159382724017646*10^-1, 1.414986880765974*10^0};
(*Heliocentric velocities of Earth and Mars (from JPL's Horizons ephemeris) on 26 November 2011, in metres*)
ve = 149597870700/86400 {-1.563974110293042*10^-2, 7.690252775639107*10^-3};
vm = 149597870700/86400 {-1.160326991502370*10^-2, -5.778933879736245*10^-3} ;
(*Hyperbolic excess velocity, in metres per second. Difference between spacecraft's Heliocentric velocity vLambert[1] and Earth's Heliocentric velocity ve*)
vinf = Norm[{-29134.32, 15779.21} - ve];
(*Earth orbital radius of departure hyperbola, in metres*)
rp = (r[1] + 300000);
(*Earth ejection angle, in radians*)
e = 6.37526
(*Interplanetary transfer trajectory model*)
(*Models the motion of Earth (xe, ye), Mars (xm, ym) and spacecraft (xsc, ysc) in a Cartesian coordinate system*)
Soln = ParametricNDSolve[{
xe''[t] == -((G ms xe[t])/(xe[t]^2 + ye[t]^2)^(3/2)),
ye''[t] == -((G ms ye[t])/(xe[t]^2 + ye[t]^2)^(3/2)),
xm''[t] == -((G ms xm[t])/(xm[t]^2 + ym[t]^2)^(3/2)),
ym''[t] == -((G ms ym[t])/(xm[t]^2 + ym[t]^2)^(3/2)),
xsc''[t] == -((G ms xsc[t])/(xsc[t]^2 + ysc[t]^2)^(3/2)) - (G me (xsc[t] - xe[t]))/((xsc[t] - xe[t])^2 + (ysc[t] - ye[t])^2)^(3/2) - (G mm (xsc[t] - xm[t]))/((xsc[t] - xm[t])^2 + (ysc[t] - ym[t])^2)^(3/2),
ysc''[t] == -((G ms ysc[t])/(xsc[t]^2 + ysc[t]^2)^(3/2)) - (G me (ysc[t] - ye[t]))/((xsc[t] - xe[t])^2 + (ysc[t] - ye[t])^2)^(3/2) - (G mm (ysc[t] - ym[t]))/((xsc[t] - xm[t])^2 + (ysc[t] - ym[t])^2)^(3/2),
xe[0] == pe[[1]], ye[0] == pe[[2]], xm[0] == pm[[1]],
ym[0] == pm[[2]], xsc[0] == pe[[1]] + (r[1] + 300000) Cos[e p],
ysc[0] == pe[[2]] + (r[1] + 300000) Sin[e p], xe'[0] == ve[[1]],
ye'[0] == ve[[2]], xm'[0] == vm[[1]], ym'[0] == vm[[2]],
xsc'[0] == ve[[1]] - Sqrt[vinf^2 + (2 G me)/rp] Sin[e p],
ysc'[0] == ve[[2]] + Sqrt[vinf^2 + (2 G me)/rp] Cos[e p]}, {xe[t],
ye[t], xm[t], ym[t], xsc[t], ysc[t]}, {t, 0, tmax}, {p},
AccuracyGoal -> 10, PrecisionGoal -> 10,
Method -> "StiffnessSwitching", MaxSteps -> 10000000]
(*Plot of interplanetary trajectory before ejection angle "fix"*)
Orbits = ParametricPlot[{{xe[t][1], ye[t][1]}, {xm[t][1], ym[t][1]}, {xsc[t][1], ysc[t][1]}} /. Soln, {t, 0, TOF}, AxesLabel -> {x, y}, ImageSize -> Large, PlotRange -> {{-0.25*10^12, 0.25*10^12}, {-0.25*10^12, 0.25*10^12}}]
(*Finding value for parameter p that will fix the Earth ejection angle and produce the desired orbital radius upon Mars intercept*)
(*Constrained spacecraft to target an orbit of 300km above Mars*)
(*Constrained time search to be 10 days before and 10 days after "ideal" intercept time TOF*)
rm = NMinimize[{(Norm[{xm[t][p], ym[t][p]} - {xsc[t][p], ysc[t][p]}] + (r[2] + 300000)) /. Soln, TOF - 10 (86400) < t < TOF + 10 (86400) && 0.8 < p < 1}, {t, p}, Method -> "NelderMead"]
(*Orbital radius above Mars's surface, in metres*)
rm[[1]] - r[2]
(*Parameter value that gives closest approach*)
pmin = Last[Last[Last[rm]]]
(*Time of closest approach, in seconds*)
tp = Last[rm[[2]][[1]]]
(*Plot of interplanetary trajectory after ejection angle "fix"*)
Orbits = ParametricPlot[{{xe[t][pmin], ye[t][pmin]}, {xm[t][pmin], ym[t][pmin]}, {xsc[t][pmin], ysc[t][pmin]}} /. Soln, {t, 0, tp}, AxesLabel -> {x, y}, ImageSize -> Large, PlotRange -> {{-0.25*10^12, 0.25*10^12}, {-0.25*10^12, 0.25*10^12}}]
(*Animation of interplanetary trajectory after ejection angle "fix"*)
OrbitAnimation = Animate[ParametricPlot[{{xe[t][pmin], ye[t][pmin]}, {xm[t][pmin], ym[t][pmin]}, {xsc[t][pmin], ysc[t][pmin]}} /. Soln /. t -> a, {t, 0, a}, AxesLabel -> {x, y}, ImageSize -> Large, PlotRange -> {{-0.3*10^12, 0.3*10^12}, {-0.3*10^12, 0.3*10^12}}], {a, 0, tmax}, AnimationRate -> 1000000]
As it stands, the optimization seems to work very well and manages to find a value for p within a few seconds that will give an orbital radius of 301.428km above Mars' surface upon intercept.
Below is the original "unfixed" trajectory:

And here is the fixed trajectory using the optimizer:
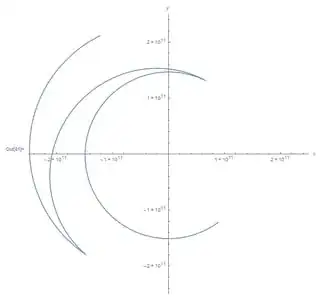
However, ParametricNDSolve uses relatively low values of AccuracyGoal -> 10 and PrecisionGoal -> 10. Tests using higher values of AccuracyGoal and PrecisionGoal produced very different results when the spacecraft came close to Mars (as seen below when the simulation was run for 1000 days) (note that the trajectories shown below were found by trial-and-error instead of using the optimizer):
Trajectory using AccuracyGoal -> 10 and PrecisionGoal -> 10:

Trajectory using AccuracyGoal -> 18 and PrecisionGoal -> 18:

As can be seen above, the two trajectory outputs are qualitatively very different and this is likely due to error accumulated when the trajectory changes rapidly as it passes close to Mars.
As such, I'm hoping to be able to use as high a value of AccuracyGoal and PrecisionGoal as possible in order to minimize error and it seems like a value of 18 would do the trick. However, when using AccuracyGoal -> 18 and PrecisionGoal -> 18 the optimizer comes to a complete standstill, and unfortunately it becomes much quicker to just calculate the Earth ejection angle correction by trial-and-error.
I'm hoping that some Mathematica experts may be able to shed some light on my horribly inefficient code, as I'm desperately hoping to not have to go back to using trial-and-error to find a trajectory fix! Any help would be greatly appreciated, and if more information is required I'll be happy to supply it. Thanks very much.
EDIT:
After reading the replies and doing a little more testing, I felt that something was very wrong. I adjusted the Mars arrival periapse distance from r[2] + 300000 (300km above Mars' surface) (this is a bit of code that sits in the NMinimize function and acts as a constraint) to an order of magnitude higher (r[2] + 3000000 or 3000km above Mars' surface) and found no difference in the output trajectory when the simulation was run for 1000 seconds (change tp to TOF in the Orbits time variable to see this). I then started to increase the arrival periapse distance by an order of magnitude iteratively until I found a change in the output trajectory. This only occurred at r[2] + 30000000000000000 which is clearly not correct!
Aside from the issue of using AccuracyGoal and PrecisionGoal instead of SetPrecision and WorkingPrecision I wonder if it's something wrong in my code or if ParametricNDSolve or NMinimize are not working correctly in this instance. It would be very helpful if someone else could possibly see if they have the same strange behavior as I did using the code.


WorkingPrecision -> 16. The general rule of thumb Mathematica uses is that thePrecisionGoal/AccuracyGoalis set (unless overidden) to one-half theWorkingPrecision. (You should increase the precision of your coefficients to matchWorkingPrecision; seeSetPrecision.) (2)FindMinimumought to be faster thanNMinimizeand might be just as reliable, if you can give it a good starting point. And minimizing the norm squared and simplifying to get rid of theAbswill let it use derivatives. – Michael E2 Jul 12 '15 at 16:51WhenEventcan be used to give a good starting point forFindMinimum(or perhaps even to find the minimum). – Michael E2 Jul 12 '15 at 18:16pin order to find the required Mars periapse intercept radius using WhenEvent? With regards to usingFindMinimum, I used initial guesses wheret = TOFandp = pminby first gettingpminfromNMinimizewithAccuracyGoal -> 10andPrecisionGoal -> 10as a rough initial guess. Unfortunately I didn't notice any appreciable time difference withAccuracyGoal -> 18andPrecisionGoal -> 18when using these initial guesses inFindMinimum. – indigoblue Jul 12 '15 at 18:29NDSolveapproach presented in this answer, http://mathematica.stackexchange.com/questions/58244/find-maximum-value-of-interpolation-function-obviously-wrong-result/58256#58256, but it sounds like it might not work here. – Michael E2 Jul 12 '15 at 18:54WorkingPrecision -> 16but this gave me the following error:The precision of the differential equation ... is less than WorkingPrecision. I'm not too sure how to fix this as the error example in the documentation doesn't seem to help unfortunately. – indigoblue Jul 12 '15 at 20:07SetPrecision[eqns, 16]. – Michael E2 Jul 12 '15 at 20:09SetPrecision[]seemed to change something, but I'm not too sure what. I commented outAccuracyGoal -> 10andPrecisionGoal -> 10and wrappedParametricNDSolveinSetPrecision[ParametricNDSolve[...], 20]since you mentioned thatAccuracyGoalandPrecisionGoalare set to half ofWorkingPrecisionif not explicitly set. I then triedSetPrecision[ParametricNDSolve[...], 40]which seemed to make no further difference at all in terms ofNMinimize'scalculation time or actualParametricPlotoutput. However, wouldn't this makeAccuracyGoal -> 20andPrecisionGoal -> 20? – indigoblue Jul 12 '15 at 21:48ParametricNDSolve[SetPrecision[eqns, 20], vars, {t, t1, t2}, params, WorkingPrecision -> 20]-- notSetPrecisionon the outside. – Michael E2 Jul 13 '15 at 04:47Norm[{xm[t][p], ym[t][p]} - {xsc[t][p], ysc[t][p]}]. That you add a constant, such(r[2] + 300000), has no impact whatsoever until the constant becomes so large that it dwarfsNorm[...]. In fact, I have deleted that constant term with no change in result, as expected. – bbgodfrey Jul 13 '15 at 16:34rmand shall post it when I return in about two hours. The trajectory to Mars is essentially unchanged, but the trajectory is very different at later times. – bbgodfrey Jul 13 '15 at 19:20PrecisionGoalandAccuracyGoalthat is getting me worried. – indigoblue Jul 13 '15 at 21:44