How to sort the ranges of a Piecewise expression?

Question

I have the following PieceWise expression

qq=
 Piecewise[{
  {x/8, x <= -6}, 
  {x/2, x >= 22 - 8*Sqrt[6]}, 
  {(1/384)*(52 + 72*x + 3*x^2), -2 <= x <= 18 - 8*Sqrt[6]}, 

  {(-14696 + 6144*Sqrt[6] + 468*x + 66*x^2 - x^3)/1536, 
       18 - 8*Sqrt[6] < x < 22 - 8*Sqrt[6]}},

  (216 + 300*x + 18*x^2 + x^3)/1536
 ]

Which Mathematica conveniently displays as

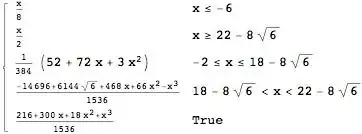
enter image description here

A manually aligned and screenshotted picture of the function and the ranges is below. The colorful picture at the bottom was produced using NumberLinePlot. Note that the NumberLinePlot displays the ranges from "bottom to top" in the order in which they appear in the Piecewise function.

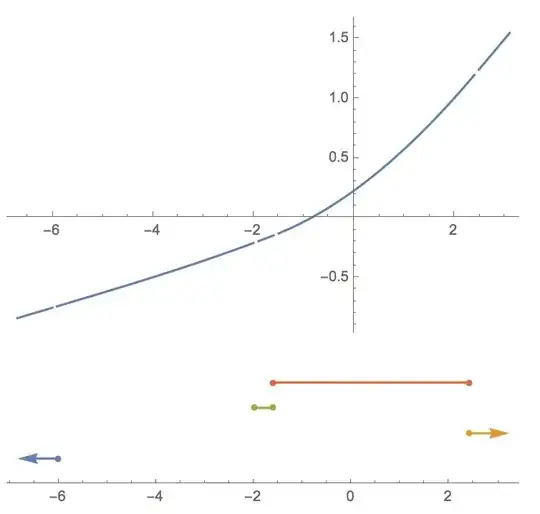
enter image description here

Is there a convenient way to sort the pieces of this expression by the range on which they are active? A convenient format would be to have only, for an increasing sequence $(a_k)_{k=0}^n$ {x<=a0,x<=a1, x<=a2 ...} in the ranges, so that the an<=x case becomes the last case, which is always True if the other cases fail. That is, the True case should correspond to the orange arrow in the picture above.

Notes

PiecewiseExpand has been used to make the expression above, which nicely isolates the x's in the inequalities.

Disclaimer: I can probably do this myself, but I think this makes for a nice question.

Try applying Internal`PiecewiseOrderless[] to your function. — J. M.'s missing motivation, Jul 14 '15 at 13:49
@Guesswhoitis. I get Internal`PiecewiseOrderless@qq == PiecewiseExpand@qq -> True. (StringSplit[#, "`"] & /@ Names["*`*Piecewise*"])[[All, -1]] // Column is interesting. — Jacob Akkerboom, Jul 14 '15 at 14:01
Damn, I thought it would sort it out; it's what I used to use for this application… — J. M.'s missing motivation, Jul 14 '15 at 14:11
@ShutaoTang that is certainly a good start. However, it is not perfect. Note that the case True still corresponds to the specification -6<=x<=-2. — Jacob Akkerboom, Jul 14 '15 at 14:37
Jacob, I have a somewhat tangential question: are you trying to achieve this sorting mostly for "aesthetic" reasons, or is there a more significant goal that I am missing? Thanks! — MarcoB, Jul 14 '15 at 16:06
@MarcoB I suppose it is mostly for aesthetic reasons, i.e. to be able to see how to function works quickly. I suppose this could also eliminate some unnecessary testing in the evaluation of the expression though. — Jacob Akkerboom, Jul 14 '15 at 16:23

Dr. belisarius · Accepted Answer · 2015-07-14T16:34:18.773

4

(* A function from the docs on RankedMax[ ] *)
PiecewiseDomains[HoldPattern[Piecewise[cases_, default_]]] :=
                 Module[{dl = Last /@ cases}, Append[dl, Not[Or @@ dl]]]

Quiet@Maximize[{x, #}, x] & /@ PiecewiseDomains[qq] // N // Ordering
(* {1, 5, 3, 4, 2} *)

Is the order of your segments, the last entry corresponding to the default case

edited Jul 14 '15 at 16:34

answered Jul 14 '15 at 15:10

Dr. belisarius

115,881
13
203
453

Great! I bet this works for any Piecewise expression that has been sanitized by PiecewiseExpand. It even deals with cases of the form x==num, which I didn't bother to ask. – Jacob Akkerboom Jul 14 '15 at 15:28

How to sort the ranges of a Piecewise expression?

1 Answers1