Symbolic area calculation for a parametric self-intersecting closed curve

Question

The parametric equation of the curve is:

$$\begin{cases} x &= -9 \sin (2 t)-5 \sin (3 t) \\[6pt] y & = 9 \cos (2 t)-5 \cos (3 t) \end{cases}\quad t\in[0,2\pi]$$

which can be easily visualized as:

The implicit form:

$$ \begin{array}{rl} F(x,y)=&625(x^2+y^2)^3-36450y(5x^4-10x^2y^2+y^4)\\ &+585816(x^2+y^2)^2-41620992(x^2+y^2)+550731776=0 \end{array} $$ It is relatively easier to obtain the numerical solution of the enclosed area.

Is it possible to find the symbolic one? The key seems to be how to find the symbolic coordinates of the self-intersection points of the curve.

Answer 1

The plan is first get the "external" contour and then use Green's theorem to find its area.

r[t_] := {-9 Sin[2 t] - 5 Sin[3 t], 9 Cos[2 t] - 5 Cos[3 t], 0}

(*find the intersections*)
tr = Quiet@ToRules@Reduce[{r@t1 == r@t2, 0 < t1 < t2 < 2 Pi}, {t1, t2}];
pt = {t1, t2} /. {tr} // Flatten;
pts = SortBy[pt, N@# &];
pps = Partition[pts, 2];

Now we can use Green's theorem to calculate the area by evaluating a line integral of a piecewise smooth function between those points. First we verify that the curve is oriented as expected:

Show[ParametricPlot[Most@r@t, {t, #[[1]], #[[2]]}, 
                    PlotRange -> {{-14, 14}, {-14, 14}}] & /@ pps] /. Line :> Arrow

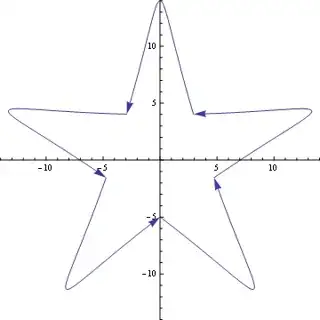
So:

(*Green's theorem, "vectorial" form*)
k[{t2_, t1_}] = Integrate[Last@Cross[r@t, r'@t], {t, t1, t2}]/2;
arean = k /@ pps;
area = Total@arean;
arean // N
area // N
(* {42.9706, 42.9706, 42.9706, 42.9706, 42.9706} *)
(* 214.853 *)

So area is composed by five numerically equivalent integrals. Let's get a symbolic form by using the first of them (the easier one to work with). You can verify that if we define:

ff[n_] := ArcTan[Sqrt@Root[1 - 2026 #1 + 67761 #1^2 - 2123042 #1^3 + 33867982 #1^4 - 
          251359006 #1^5 + 1020220287 #1^6 - 2365497302 #1^7 + 3139485186 #1^8 - 
          2365497302 #1^9 + 1020220287 #1^10 - 251359006 #1^11 + 33867982 #1^12 - 
          2123042 #1^13 + 67761 #1^14 - 2026 #1^15 + #1^16 &, n]];

then

 arean[[1]] == -((252*Sqrt[3*(-68561 + 5154*Sqrt[181])])/3125) - 174*(ff[1] - ff[2])

which is one fifth of the symbolic result you're after.

---

We may try to quickly verify if the result is reasonable by doing some image processing. We'll use a somewhat large image size (3000 pxs width) to get some accuracy:

lims = {-1, 1} + # &/@ N@Outer[#2[#1, t] &, Most@r@t, {MinValue, MaxValue}];

img = Show[ParametricPlot[a Most@r@t, {t, #[[1]], #[[2]]}, {a, 0, 1}, 
           PlotRange -> lims, Axes -> False, Mesh -> False, Frame -> False,
           ImageSize -> 3000] & /@ Partition[pts, 2]];

And now we count colored and white pixels

counts = Last /@ (ImageData[Binarize@img] // Flatten // Tally)
(* {6228712, 2366288} *)

And comparing the the area quotients calculated by both methods:

Times @@ (Subtract @@@ lims)/area // N
(* 3.64587 *)

Tr@counts/counts[[2]] // N
(* 3.63227 *)

we see that the results agree within reasonable limits

Answer 2

Although Belisarius' creative solution is entirely satisfactory, a solution symbolic at every step may be useful. To begin, define

x[t_] := -9 Sin[2 t] - 5 Sin[3 t]
y[t_] :=  9 Cos[2 t] - 5 Cos[3 t]

and note that t = π corresponds to the uppermost point in the star in the question, {0, 14}}. From there, the point {0, -5} can be reached by increasing or decreasing t by 2 π/5 + t0, where t0 is the change in t from the uppermost point to the nearest points at which two curve segments intersect. This quantity is obtained by,

Solve[x[π + t] - x[π - t] == 0, t] /. C[1] -> 0;
t0 = %[[4, 1, 2]] - 2 π/5
(* (3 π)/5 + ArcTan[(2 Sqrt[15 (5 - 3/10 (9 - Sqrt[181]))])/(9 - Sqrt[181])] *)

(This simple derivation is based on the solution by Michael E2 to question 33947, as highlighted by Shutao Tang in a comment above.) Then, following Belisarius, we apply Green's Theorem.

5/2 Integrate[(y[t] D[x[t], t] - x[t] D[y[t], t]), {t, Pi + t0, Pi - t0}]
      // TrigExpand // FullSimplify
(* -(252/625) Sqrt[3 (-68561 + 5154 Sqrt[181])] + 261 π - 
       435 ArcCot[Sqrt[1/33 (-79 + 6 Sqrt[181])]] *)

The numerical value of this answer is 214.853, as expected.