How do I generate n random numbers with an extra condition

Question

I need to generate n random numbers that would sum into a. And I can't find an elegant solution here: https://reference.wolfram.com/language/tutorial/RandomNumberGeneration.html .

The only solution I have in my head is to generate random numbers and than include IF sentence. But it would take years before Mathematica would find the n random numbers whose sum is exactly a. Any other ideas on how to do this here?

Answer 1

To be able to answer this question, we need to agree what "random" means precisely. To me, the most reasonable interpretation is to require a uniform distribution on the $\sum_i x_i = a$ simplex.

This will be satisfied by Praan's solution once we filter tuples containing negative numbers. Let's illustrate using $a=1$ and $n=3$.

Praan's method:

pts = Select[
   Append[#, 1 - Total[#]] & /@ RandomReal[1, {10000, 2}],
   Positive[Times @@ #] &
   ];

ListPointPlot3D[
 pts,
 BoxRatios -> {1, 1, 1}
 ]

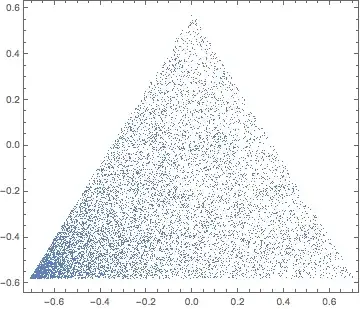
Or let's just project down to 2D to make things easier to see:

Appropriate basis vectors:

a = Normalize[{-1, 1, 0}];
b = Normalize[{-1, -1, 1}];

ListPlot[
 {a.#, b.#} & /@ pts,
 AspectRatio -> Automatic,
 Axes -> False, Frame -> True
 ]

The fact that the distribution will be uniform is also clear from the fact that this method is effectively doing a linear transformation on points of the form $(x,y,0)$, which are already uniformly distributed within a plane.

ciao's idea (comments) gives a very different distribution:

pts = Table[
   Normalize[RandomReal[{0, 1}, 3], Total],
   {10000}
   ];

And Simon Rochester's method (comments) produces a distribution that's different from both:

pts = Table[
   Differences@Append[NestList[# + RandomReal[{0, 1 - #}] &, 0, 2], 1],
   {10000}
   ];

To decide which one is right, we need to agree on the interpretation of random. To me, the most reasonable interpretation is this: a "random triplet of numbers" means uniform distribution in 3D Euclidean space. Adding a constraint (i.e they must sum to $a$) should not modify this requirement, i.e. that we need to have uniform distribution in 3D Euclidean space.

This is only satisfied by Praan's method.

Answer 2

Generate $n-1$ random numbers first. Then the $n$th number is given by $a$ minus the sum of the $n-1$ randomly generated numbers. Your code could look like this, for example,

rTable = RandomReal[{rmin, rmax}, n-1]
AppendTo[rTable, a-Total@rTable]
a == Total@rTable

Edit

As pointed out by Szabolcs in the comments of this answer, this method fails when the $n$-th number is negative since the OP requested positive numbers (for suitable $a$ and $n$). This can be remedied by selecting only those lists of random numbers where the $n$-th number is positive.

For a nice implementation, see the answer of Szabolcs, in which the question is reformulated in terms of a uniform distribution on the $(n-1)$-simplex defined by $\sum_{i=0}^{n-1}x_i/a=1$.