How to simplify 1 - Cos[2x] to 2 Sin[x]^2?

Question

I want to reduce all Cos[2 x] to 1 - 2Sin[x]^2, it seems Mathematica will always simplify 2 Sin[x]^2 to 1 Cos[2x], but how to do the reverse?

Answer 1

One way will be to add it to the definition of Cos by Unprotecting it.

Unprotect[Cos]
Cos[2 x] := 1 - 2 Sin[x]^2
Protect[Cos]

Then evaluating the following:

2 Cos[2 x] + 3 x Cos[2 x] + Tan[x] Sin[x] Cos[2 x] + Exp[Tan[Cos[2 x]]]

gives:

Which you can further Simplify if you so please. Notice that the desired replacement has occurred everywhere there's Cos[2x]

Answer 2

Expanding Cos[2 x] to 1 - Sin[x]^2 and simplifying are somewhat opposite procedures. Simplify basically reduces the leaf count (see How do I invoke the default complexity function? for more details). As we can see the number of leaves in the goal is twice the numbers of leaves in the starting expression:

LeafCount /@ {Cos[2 x], 1 - Sin[x]^2}
(*  {4, 8}  *)

TreeForm /@ {Cos[2 x], 1 - Sin[x]^2} // GraphicsRow

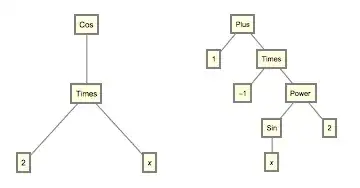
The basic built-in function for performing the sort transformation the OP desires is TrigExpand. But TrigExpand applies a different identity to Cos[2 x] than the desired one:

TrigExpand[Cos[2 x]]
(*  Cos[x]^2 - Sin[x]^2  *)

This may be acceptable, since it is one of the three common forms of the double-angle identity. Generally, I try to figure out how Mathematica works and adapt my thinking to conform -- that is, I try to learn how to use the tool in the way it was designed to be used and to work with the tool and not against it. But Mathematica is a quite flexible tool, so if the identity in terms of Sin[x] only is desired, it is possible to use it.

One could replace Cos[x]^2 by 1 - Sin[x]^2 in the output of TrigExpand as suggested in a comment by Stefan R. One could also replace Cos[2 x] by 1 - Sin[x]^2 directly. This seems the simplest way.

Cos[2 x] /. {Cos[2 t_] :> 1 - 2 Sin[t]^2}
(*  1 - 2 Sin[x]^2  *)

---

In a complicated expression like RunnyKine's, the possible goals ramify. TrigExpand does a really bad job (image) as evaluated by a human-readable aesthetic. If we make the expression slightly more complicated with a Cos[4 x],

expr = 2 Cos[4 x] + 3 x Cos[2 x] + Tan[x] Sin[x] Cos[2 x] + Exp[Tan[Cos[2 x]]];

then is the goal to expand only Cos[2 x], like this?

expr /. {Cos[2 t_] :> 1 - 2 Sin[t]^2}
(*
  E^Tan[1 - 2 Sin[x]^2] + 2 Cos[4 x] +            <-- N.B. Cos[4 x]
   3 x (1 - 2 Sin[x]^2) + Sin[x] (1 - 2 Sin[x]^2) Tan[x]
*)

Or should we expand all cosines with an even coefficient, like this?

expr //.                                      (*  <-- N.B. ReplaceRepeated  *)
 {Cos[a_Integer?EvenQ t_] :> 1 - 2 Sin[a t/2]^2}
(*
  E^Tan[1 - 2 Sin[x]^2] + 3 x (1 - 2 Sin[x]^2) +
   2 (1 - 2 Sin[2 x]^2) +                         <-- N.B. Sin[2 x]
   Sin[x] (1 - 2 Sin[x]^2) Tan[x]
*)

Or maybe the goal is to convert all sines and cosines to terms of Sin[x], unless there are leftover terms of Cos[x], which can be done like this:

expr //.
 {Cos[a_Integer?EvenQ t_] :> 1 - 2 Sin[a t/2]^2, 
  Sin[a_Integer?EvenQ t_] :> 2 Sin[a t/2] Cos[a t/2],
  Cos[t_]^(p_Integer?EvenQ) :> (1 - Sin[t]^2)^(p/2)}
(*
  E^Tan[1 - 2 Sin[x]^2] + 3 x (1 - 2 Sin[x]^2) + 
   2 (1 - 8 Sin[x]^2 (1 - Sin[x]^2)) + Sin[x] (1 - 2 Sin[x]^2) Tan[x]
*)

And what, if anything, to do about Tan[x]?

Answer 3

You could go ahead and modify the mathematica output manually by defining exactly what you want to have transformed. In your case this would look like this:

MakeBoxes[Cos[2*x_], StandardForm] := RowBox[{MakeBoxes[1 - 2 Sin[x]^2]}];

This effectively turns every occurrence of Cos[2x] in StandardForm into 1 - 2 Sin[x]^2. I use this to get a certain standard notation for dirac delta functions.