Poor/wrong sampling in 1D DiscretizeRegion of splines?

Question

Bug introduced in 10.1 and fixed in 11.3

Context

In relation to this question I have would like to use splines to define a ParametricRegion and DiscretizeRegion

I proceed as follows:

pts = {{1, 0}, {1.8, 3}, {0, 2}};
 {xu, yu} = Transpose[pts]; 
n = 2;m = Length[pts]; 
knots = {ConstantArray[0, n + 1], Range[m - n - 1]/(m - n), 
         ConstantArray[1, n + 1]} // Flatten; 
fx[t_] = xu.Table[ BSplineBasis[{n, knots}, i - 1, t], {i, Length[pts]}]; 
fy[t_] = yu.Table[ BSplineBasis[{n, knots}, i - 1, t], {i, Length[pts]}];

So that

ParametricPlot[{fx[t], fy[t]}, {t, 0, 1}, Axes -> None, Frame -> True,
  Epilog -> {Directive[AbsolutePointSize[5], Red], Point[pts]}]

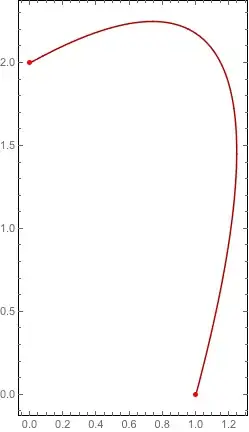
Mathematica graphics

Now I would like to Discretize this BSpline as follows:

  dpr = ParametricRegion[{{ fx[t], fy[t]}, 0 <= t <= 1}, t];
  δΩ = DiscretizeRegion[dpr, MaxCellMeasure -> 0.001];

This seems to produce a buggy region. Indeed

   Show[δΩ, Axes -> True]

Mathematica graphics

presents some defect in the triangulation. Note in particular the two points at the origin and at coordinate (0.9,-0.2).

Question

Is this a bug in DiscretizeRegion?

Can anyone reproduce this problem?

I am using mathematica 10.1 on macos X.

Thanks!

Update

In mathematica 10.2 is works better but not always. For instance let us define

 << NDSolve`FEM`
Jet0[pts_: {{1, 0}, {1.8, 1.8}, {0, 2}}] := 
 Module[{xu, yu, n, m, knots, fx, fy, pr, mesh, t, r},
  {xu, yu} = Transpose[pts];
  n = 2; m = Length[pts];
  knots = {ConstantArray[0, n + 1], Range[m - n - 1]/(m - n), 
     ConstantArray[1, n + 1]} // Flatten;
  fx[t_] = 
   xu.Table[BSplineBasis[{n, knots}, i - 1, t], {i, Length[pts]}];
  fy[t_] = 
   yu.Table[BSplineBasis[{n, knots}, i - 1, t], {i, Length[pts]}];
  pr = ParametricRegion[{{r fx[t], r fy[t]}, 0 <= t <= 1 && 
      0 <= r <= 1}, {t, r}];
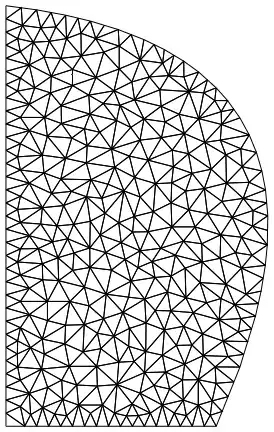
  mesh = ToElementMesh[pr, "MaxBoundaryCellMeasure" -> 0.1];
  mesh["Wireframe"]]

so that

Jet0[]

produces

Mathematica graphics

but on the other hand

Jet0[{{1, 0}, {1.8, 1.8}, {0, 3}}]

produces

$Failed[Wireframe]

I can reproduce this on Windows in 10.1 but it has been fixed in 10.2. — RunnyKine, Jul 26 '15 at 20:21
@RunnyKine thanks! Do you think it is the source of my problem in the linked question? Should I retag my question as bug? as 10.1? — chris, Jul 26 '15 at 20:27
I don't think that's the source of the problem. If you can rewrite the ParametricRegion as an ImplicitRegion you may have better chances. For some reason, Mathematica doesn't know how to handle ParametricRegion properly. — RunnyKine, Jul 26 '15 at 20:42
"convert to ImplicitRegion[]" - should be doable via PiecewiseExpand[] and a few other functions, but since it's piecewise polynomial, you will have to tack on not a few inequalities to restrict the domain. Just describing the route makes me shudder… — J. M.'s missing motivation, Jul 27 '15 at 18:57
Refs for tagging bugs: http://meta.mathematica.stackexchange.com/a/1611, http://meta.mathematica.stackexchange.com/a/83 — Michael E2, Jul 27 '15 at 19:48
DiscretizeRegion[pr, MaxCellMeasure -> {"Length" -> 0.1}] works in V10.2. -- This also works, ToElementMesh[BoundaryDiscretizeRegion[pr, MaxCellMeasure -> {"Length" -> 0.1}]] and gives a warning that might be significant. — Michael E2, Jul 27 '15 at 19:54
Including the word "fixed" on the first line is going to make this post disappear from the bug-radar. — Szabolcs, Jul 27 '15 at 20:14
@Szabolcs what do you suggest? Its a bug with an easy workaround? — chris, Jul 27 '15 at 20:23
I think there's an error in Jet0: Should it read 0 <= t <= 1 instead of -1 <= t <= 1 in ParametricRegion? (Doesn't fix problem, though, it seems.) — Michael E2, Jul 27 '15 at 20:26
@MichaelE2 yes you are right. I had corrected it but not online :-) — chris, Jul 27 '15 at 20:29
@Michael, BSplineBasis[] zeroes out outside $[0,1]$, but it's better that you corrected @chris. ;) — J. M.'s missing motivation, Jul 27 '15 at 20:36
@Guesswhoitis. Yes, and I was hoping that was the source of the problem, but alas.... — Michael E2, Jul 27 '15 at 20:38
This seems fixed in V11.3. Can you confirm that Chris? Thanks. — user21, Jan 28 '19 at 09:23

score 6 · Answer 1 · answered Jul 27 '15 at 19:52

There is a workaround involving Rationalize.

Jet0[pts0_: {{1, 0}, {1.8, 1.8}, {0, 2}}] := 
 Module[{xu, yu, n, m, knots, fx, fy, pr, mesh, t, r},
   pts=Rationalize[pts0,0.001];
  {xu, yu} = Transpose[pts];
  n = 2; m = Length[pts];
  knots = {ConstantArray[0, n + 1], Range[m - n - 1]/(m - n), 
     ConstantArray[1, n + 1]} // Flatten;
  fx[t_] = 
   xu.Table[BSplineBasis[{n, knots}, i - 1, t], {i, Length[pts]}];
  fy[t_] = 
   yu.Table[BSplineBasis[{n, knots}, i - 1, t], {i, Length[pts]}];
  pr = ParametricRegion[{{r fx[t], r fy[t]}, -1 <= t <= 1 && 
      0 <= r <= 1}, {t, r}];
  mesh = ToElementMesh[pr, "MaxBoundaryCellMeasure" -> 0.1];
  mesh["Wireframe"]]

works as expected:

 Jet0[{{1, 0}, {1.8, 1.8}, {0, 3}}]

Mathematica graphics

I thought the error with BoundaryDiscretizeRegion suggested a numerical issue. +1 — Michael E2, Jul 27 '15 at 20:06

Michael E2 · Accepted Answer · 2015-07-27T20:30:49.907

4

DiscretizeRegion will work in place of ToElementMesh:

Jet0[pts_: {{1, 0}, {1.8, 1.8}, {0, 2}}] := 
 Module[{xu, yu, n, m, knots, fx, fy, pr, t, r},
  {xu, yu} = Transpose[pts];
  n = 2; m = Length[pts];
  knots = {ConstantArray[0, n + 1], Range[m - n - 1]/(m - n), 
     ConstantArray[1, n + 1]} // Flatten;
  fx[t_] = xu.Table[BSplineBasis[{n, knots}, i - 1, t], {i, Length[pts]}];
  fy[t_] = yu.Table[BSplineBasis[{n, knots}, i - 1, t], {i, Length[pts]}];
  pr = ParametricRegion[{{r fx[t], r fy[t]}, 0 <= t <= 1 && 0 <= r <= 1},
        {t, r}];
  DiscretizeRegion[pr, MaxCellMeasure -> {"Length" -> 0.1}]]

Jet0[{{1, 0}, {1.8, 1.8}, {0, 3}}]

Mathematica graphics

edited Jul 27 '15 at 20:30

answered Jul 27 '15 at 20:04

Michael E2

235,386
17
334
747

1

your answer is useful for people who are happy with DiscretizeRegion. According to @user21 I need ToElementMesh in order to be able to solve a PDE on it. – chris Jul 27 '15 at 20:11
1

@chris ToElementMesh@Jet0[{{1, 0}, {1.8, 1.8}, {0, 3}}] generally converts a MeshRegion to an ElementMesh with no problem. NDSolve should convert a MeshRegion automatically, too, but often one wants to set up the ElementMesh first before calling NDSolve. (The problem here is getting from a parametric description to any sort of mesh.) – Michael E2 Jul 27 '15 at 20:15
2

@chris, Ayy, I forgot there is a difference: Along the boundary, the quadratic vertices in converting a MeshRegion are placed on the linear boundary elements; in converting a Region, they are placed on the Region's boundary and thus are more accurate for solving PDEs. – Michael E2 Jul 27 '15 at 20:45
3

@MichaelE2, yes this is quite an important point, For numerics ToElementMesh is preferable. – user21 Jul 28 '15 at 07:12

Poor/wrong sampling in 1D DiscretizeRegion of splines?

Context

Question

Update

2 Answers2

Linked