I'm drawing the magnetic field lines of a rotating dipole (magnetic field distorded by emission of radiation). Currently, my Mathematica 7.0 code is fully working, but I'm having a constraint which I don't know how to solve in a proper way: All the field lines I want to show should be tangent to the "light cylinder" surrounding the rotating dipole.
That means that the magnetic field vector $\bf B$ should be orthogonal to the cylinder's normal, located at $x^2 + y^2 = 1$ (the "light cylinder" have a radius of 1, in the code below) :
$\quad \quad {\bf B \cdot n} = 0$.
In the code below (for a simple non-rotating tilted dipole, to save space here), the field lines are starting on the surface of a sphere of radius omega < 1. The dipolar magnetic axis is tilted with an angle alpha, relative to the cylinder's axis. Take note that the constants alpha and omega are the two parameters of the field.
Using spherical coordinates theta and phi on the sphere (around the magnetic axis), I defined 30 starting points to grow the field lines from the sphere. The angle phi is uniformly distributed around the magnetic axis, but the theta angle is actually unknown. In the code below, I defined the theta angle by trial and error and this is what I want to fix.
So here's the code :
alpha=40Pi/180;
omega=2Pi (10000)/(299792458*0.001);
Mu0={Sin[alpha],0,Cos[alpha]};
r[x_,y_,z_]:=Sqrt[x^2+y^2+z^2]
Bdipolaire[x_,y_,z_]:=3(Mu0.{x,y,z}){x,y,z}/r[x,y,z]^5-Mu0/r[x,y,z]^3
NormeB[x_,y_,z_]:=Sqrt[Bdipolaire[x,y,z].Bdipolaire[x,y,z]]
Bx[x_,y_,z_]:={1,0,0}.Bdipolaire[x,y,z]
By[x_,y_,z_]:={0,1,0}.Bdipolaire[x,y,z]
Bz[x_,y_,z_]:={0,0,1}.Bdipolaire[x,y,z]
Angles:=
{0.1972815, 0.1988315,0.2014215,0.2049765,0.2090015,0.2127115,0.2151015,
0.2151015,0.2116515,0.2031515,0.1692915,0.1687315,0.1705015,0.1723815,
0.1742015,0.1759465,0.1776115,0.1792415,0.1808415,0.1824015,0.1839215,
0.1854085,0.1868585,0.1882765,0.1897015,0.1911415,0.1926035,0.1940415,
0.1953345,0.1963365}
NCourbes:=Length[Angles]
theta[n_]:= Angles[[n]]
phi[n_]:=(n-1)2Pi/NCourbes
CourbeMagnetique[n_]:=NDSolve[{
x'[s]==Bx[x[s],y[s],z[s]]/NormeB[x[s],y[s],z[s]],
y'[s]==By[x[s],y[s],z[s]]/NormeB[x[s],y[s],z[s]],
z'[s]==Bz[x[s],y[s],z[s]]/NormeB[x[s],y[s],z[s]],
x[0]==omega (Sin[theta[n]]Cos[phi[n]]Cos[alpha]+Cos[theta[n]]Sin[alpha]),
y[0]==omega Sin[theta[n]]Sin[phi[n]],
z[0]==omega (Cos[theta[n]]Cos[alpha]-Sin[theta[n]]Cos[phi[n]]Sin[alpha])
},
{x,y,z}, {s,-1/omega,1/omega},
Method->Automatic,MaxSteps->10000000,
StoppingTest->(Sqrt[x[s]^2+y[s]^2+z[s]^2]<omega)]
Do[CourbeMagnetique[n],{n,1,NCourbes}]
Smin[n_]:=(x/.CourbeMagnetique[n])[[1]][[1]][[1]][[1]]
Smax[n_]:=(x/.CourbeMagnetique[n])[[1]][[1]][[1]][[2]]
GraphicSize:=1.5
GrapheMagnetique[n_]:=
ParametricPlot3D[
Evaluate[{x[s],y[s],z[s]}/.CourbeMagnetique[n]],
{s,Smin[n],Smax[n]},
PlotStyle->{Directive[AbsoluteThickness[1]],Blue},
MaxRecursion->7,PerformanceGoal->"Quality"]
CercleLumiere:=
ParametricPlot3D[{Cos[p],Sin[p],0},{p,0,2Pi},
PlotStyle->{Directive[Thick,RGBColor[0.40,0.70,0.40]]},
PerformanceGoal->"Quality"]
AxesCartesiens=
{Line[GraphicSize {{-1,0,0},{1,0,0}}],
Line[GraphicSize {{0,-1,0},{0,1,0}}],
Line[GraphicSize {{0,0,-1},{0,0,1}}]};
AxeMagnetique=
Line[(2/3){{-Sin[alpha],0,-Cos[alpha]},{Sin[alpha],0,Cos[alpha]}}];
AxeRotation=Line[(1/3){{0,0,-1},{0,0,1}}];
AxesReference:=
Graphics3D[{
{Thin,GrayLevel[0.7],Dashed,AxesCartesiens},
{Thick,Blue,AxeMagnetique},
{Thick,RGBColor[0.40,0.70,0.40],AxeRotation}}]
Pulsar:=Graphics3D[Sphere[{0,0,0}, omega]]
Graphique=
Show[
Table[GrapheMagnetique[n],{n,1,NCourbes}],CercleLumiere,AxesReference,Pulsar,
PlotRange->{
{-GraphicSize,GraphicSize},
{-GraphicSize,GraphicSize},
{-GraphicSize,GraphicSize}},
Boxed->False,Axes->False,Lighting->"Neutral",
SphericalRegion->True,ViewPoint->{0,0,1}]
I would like to post a nice picture here to show what I'm trying to achieve, but that new picture upload interface don't allow me to upload a picture (what the hell!? Safari isn't supported?)
EDIT : Here's the picture I made with my handmade (madness) theta angles :

And here's another one for another alpha angle:
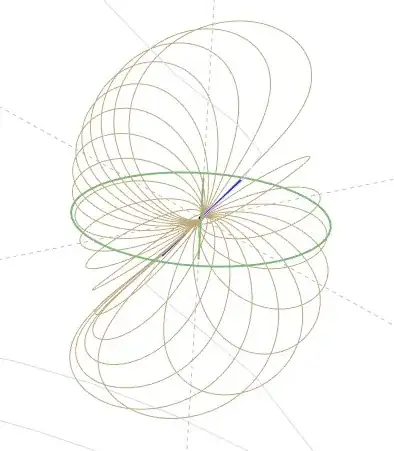
Pictures decription: The green circle is the light cylinder's equator. The green vertical axis is the symetry (rotation) axis. The blue line is the magnetic axis. Each curve on these pictures is tangent to the light cylinder. To achieve this, I need some proper theta angles for the field line starting point, around the magnetic axis.
Now, my question is this: how can I modify the code above so that Mathematica 7.0 calculates the proper 30 theta starting angles that makes the field lines tangent to the light cylinder, from the alpha and omega inputs?
Currently, I need to calculate all the theta angles myself using a painfull trial and error method, and was able to do it (very laboriously) for 5 alpha values (30, 40, 45, 60, 90 degrees) and 1 omega value only. This is madness!
EDIT 2 : For what it's worth, it can be shown that the theta angle that gives a field line tangent to the light cylinder is relatively close to $\arcsin{\sqrt{\omega}}$ :
$\quad\quad \theta = \arcsin{\sqrt{\omega}} + \delta\theta$.
When I've found the $\theta$ angles with my brute and painfull method, I was varying the angle around $\arcsin{\sqrt{\omega}}$ (for each value of $\phi$) and was evaluating the value of the scalar product $\mathcal{P} \equiv \bf B \cdot \bf n$ :
$\quad\quad \mathcal{P} = B_x(\cos{\phi'}, \, \sin{\phi'}, \, z) \cos{\phi'} + B_y(\cos{\phi'}, \, \sin{\phi'}, z) \sin{\phi'}$.
Here, $\phi'$ is the azimutal angle defined on the equator (or on the light cylinder), not around the magnetic axis, while $\phi$ is defined around the magnetic axis.
When $\mathcal{P}$ was far away from 0, I made another variation of $\theta$, until $\mathcal{P}$ was "close enough" to 0. Then I got the $\theta$ angle, for a given $\phi$. Remember that the two angles defined in my code above (theta $\equiv \theta$ and phi $\equiv \phi$) are defined on the sphere of radius omega $\equiv \omega$, around the tilted magnetic axis.
Maybe something similar could be done automatically with Mathematica ?

