How to implement a more efficient inverse triangular recursion?

Question

Consider the following inverse triangular formula

$$\left( \begin{array}{ccccc} & & & & N_{i-p,p}\left(u_0\right) \\ & & N_{i-2,2}\left(u_0\right) & & \\ & N_{i-1,1}\left(u_0\right) & & & \\ \color{red}{N_{i,0}\left(u_0\right)=1} & & N_{i-1,2}\left(u_0\right) & \cdots & \vdots \\ & N_{i,1}\left(u_0\right) & & & \\ & & N_{i,2}\left(u_0\right) & & \\ & & & & N_{i,p}\left(u_0\right) \end{array} \right)$$

where, $N_{i,0}=1$, and enter image description here

In addition, $u_0 \in [u_i,u_{i+1})$ knots = $\{u_0,u_1, \cdots, u_m\}, 0\leq u_i \leq u_j$

Here is a procedural implementaion calculate $\color{blue}{N_{i-p,p}(u_0),B_{i-p+1,p}(u_0), \cdots, N_{i,p}(u_0)}$

Search the index $i$ by the auxiliary function searchSpan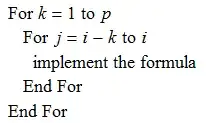

In the code, I use the following local array to store the values of $N_{m,n}$

$$ \left( \begin{array}{ccccc} & & & & N_{i-p,p}\left(u_0\right) \\ & & & & \\ & & N_{i-2,2}\left(u_0\right) & & \vdots \\ & N_{i-1,1}\left(u_0\right) & N_{i-1,2}\left(u_0\right) & \cdots & \\ N_{i,0}\left(u_0\right) & N_{i,1}\left(u_0\right) & N_{i,2}\left(u_0\right) & \cdots & N_{i,p}\left(u_0\right) \end{array} \right)_{(p+1)\times (p+1)} $$

where $N_{m,n}$ was stored in the position $(p+1-i+m,n+1)$ of local array

Search the index of span $[u_i,u_{i+1})$

searchSpan[{deg_, knots_}, u0_] :=
 Module[{biSearch},
  biSearch =
   Function[{low, high},
    With[{mid = Floor[(low + high)/2]}, 
     If[u0 < knots[[mid]], {low, mid}, {mid, high}]]
   ];(*Do bisection search*)
  First@
   NestWhile[
    biSearch[Sequence @@ #, u0] &,
    {deg + 1, Length@knots - deg}, Subtract @@ # != -1 &] - 1
]

NonzeroBasis[{deg_, knots_}, u0_] :=
 Module[{coeff, basis, i},
  coeff =
   (u0 - knots[[#1 + 1]])/(knots[[#1 + #2 + 1]] - knots[[#1 + 1]]) &;
  basis = ConstantArray[1, {deg + 1, deg + 1}];
  i = searchSpan[{deg, knots}, u0];
  Do[
   basis[[deg + 1 - k, k + 1]] =
    (1 - coeff[i - k + 1, k]) basis[[deg + 2 - k, k]];
   With[{m = deg + 1 - i},
    Do[
     basis[[m + j, k + 1]] =
      {coeff[j, k], 1 - coeff[j + 1, k]}.{basis[[m + j, k]], basis[[m + j + 1, k]]},
     {j, i - k + 1, i - 1}]
    ];
   basis[[deg + 1, k + 1]] =
    coeff[i, k] basis[[deg + 1, k]],
   {k, deg}];
   basis
 ]

Test

knots = {0, 0, 0, 0, 0, 1, 2, 3, 4, 4, 5, 6, 7, 8, 9, 10, 10, 10, 10, 10};
deg = 4;
NonzeroBasis[{deg, knots}, 5/2] // MatrixForm

$\left( \begin{array}{ccccc} 1 & 1 & 1 & 1 & \frac{1}{288} \\ 1 & 1 & 1 & \frac{1}{48} & \frac{227}{1152} \\ 1 & 1 & \frac{1}{8} & \frac{23}{48} & \frac{205}{384} \\ 1 & \frac{1}{2} & \frac{3}{4} & \frac{15}{32} & \frac{25}{96} \\ 1 & \frac{1}{2} & \frac{1}{8} & \frac{1}{32} & \frac{1}{192} \end{array} \right)$

Performance test

knots0 = 
 Join[ConstantArray[0, 3001], Range[1, 5000], ConstantArray[5001, 3001]];
deg0 = 3000;
NonzeroBasis[{deg0, knots0}, 2.5]; // AbsoluteTiming

enter image description here

Question

How to implement this triangular formula in a non-procedural(like functional or rule-based) method?
How to improve the efficience of NonzeroBasis?

Update

Another example I found today was the calculation of Bernstein function

$$B_{n,i}(u)=\binom n i u^i(1-u)^{n-i}$$, where $0 \leq u \leq 1$

In addition, Bernstein function owns the following recursive relationship:

$$B_{n,i}(u)=(1-u) B_{n-1,i}(u)+uB_{n-1,i-1}(u)$$

where, $B_{n,i}(u)=0$ when $i<0$ or $i>n$

So we can use the following triangular schematic digram to calculate $\color{blue}{B_{n,0}(u),B_{n,0}(u), \cdots, B_{n,n}(u)}$

$$\left( \begin{array}{ccccc} \text{} & \text{} & \text{} & \text{} & B_{n,0} (u) \\ \text{} & \text{} & \text{} & .\cdot{}^{\cdot} & \text{} \\ \text{} & \text{} & B_{2,0}(u)& \text{} & \text{} \\ \text{} & B_{1,0} (u) & \text{} & \text{} & \text{} \\ \color{red}{B_{0,0} (u)=1} & \text{} & B_{2,1}(u)& \vdots & \vdots \\ \text{} & B_{1,0}(u) & \text{} & \text{} & \text{} \\ \text{} & \text{} & B_{2,2}(u)& \text{ } & \text{} \\ \text{} & \text{} & \text{} & \ddots & \text{} \\ \text{} & \text{} & \text{} & \text{} & B_{n,n} (u) \\ \end{array} \right)$$

Related question

I find your explanation confusing. Not blaming, perhaps I just need another point of view. Do you perchance have any link explaining the "inverse triangular recursion"? — Dr. belisarius, Aug 14 '15 at 12:08
@belisarius, Sorry for my confusing description. In J.M's question, triangular recursion owns the following style $$\begin{array}{}T_0^{(0)}&T_1^{(0)}&T_2^{(0)}&T_3^{(0)}\T_0^{(1)}&T_1^{(1)}&T_2^{(1)}&\T_0^{(2)}&T_1^{(2)}&&\T_0^{(3)}&&&\end{array}$$So I add a prefix inverse before the triangular recursion to distinguish them. — xyz, Aug 14 '15 at 12:12
@xzczd, (1) Yes, knots is always a sorted vector that owns the style ${u_0,u_1,\cdots, u_m}$, where, $0 \leq u_i \leq u_j$ (2) No, theMachinePrecisionreal number could be used. In addition, I tried the Compile, but it failed. — xyz, Aug 16 '15 at 10:05

score 7 · Accepted Answer · edited Jun 16 '20 at 09:23

Well, to be honest, despite I've been using Mathematica for 3 years, I'm getting more and more confused about what's functional programming, but the following solution is at least more elegant and faster than yours:

searchSpan2[knots_, u0_] := First@Ordering[UnitStep[u0 - knots], 1] - 1
NonzeroBasis2[p_, u_, u0_] :=
 With[
  {i = searchSpan2[u, u0],
   coeff = (u0 - u[[#1]])/(u[[#1 + #2]] - u[[#1]]) &},
  FoldList[
   MapThread[Dot, {#2, Partition[#, 2, 1, {-1, 1}, 0]}] &,
   {1}, Table[{coeff[j, k], 1 - coeff[j + 1, k]}, {k, 1, p}, {j, i - k, i}]
  ]
 ]
NonzeroBasis[{deg0, knots0}, 2.5]; // AbsoluteTiming
NonzeroBasis2[deg0, knots0, 2.5]; // AbsoluteTiming
(* {76.629522, Null} )
( {35.073471, Null} *)

Notice that the output of my searchSpan2 equals to that of searchSpan2 plus 1, and the result is a triangular array, which can't be compiled directly.

Then, for the performance part, I failed to figure out how to compile your NonzeroBasis, but managed to write a compiled version myself:

NonzeroBasis3 =
  ReleaseHold[
   Hold@
     Compile[{{p, _Integer}, {u, _Real, 1}, {u0, _Real}}, 
      With[{i = searchSpan2[u, u0]},
       Module[{lst = Table[0., {i + 1}, {p + 1}]},
        lst[[i, 1]] = 1.;
        Do[
         lst[[j, k + 1]] = 
          (u0 - u[[j]])/(u[[j + k]] - u[[j]]) lst[[j, k]] + 
          (1 - (u0 - u[[j + 1]])/(u[[j + k + 1]] - u[[j + 1]])) lst[[j + 1, k]], 
         {k, p}, {j, i - k, i}];
        lst]
       ]
     ] /. DownValues@searchSpan2];
NonzeroBasis3[deg0, knots0, 2.5]; // AbsoluteTiming
(* {1.093708, Null} *)

Notice the structures of the results are not the same:

MatrixForm /@ Through[{NonzeroBasis[{#, #2}, #3] &, 
                       NonzeroBasis2, NonzeroBasis3}[deg, knots, 5/2]] // Row

Update

OK, seems that I'm a little tired yesterday, your NonzeroBasis isn't hard to compile, we just need to:

Take the pure function coeff out of Compile and introduce it with a With outside. Pure function can be used in Compile, but it can't exist on its own. The type of variables inside Compile is limited to _Integer, _Real, _Complex, True|False, Just as the arguments of it.
Change the ConstantArray[1, {deg + 1, deg + 1}] into ConstantArray[1., {deg + 1, deg + 1}] because basis should be a Real type array. (ConstantArray isn't compiled actually but it's not a big deal here. You can use Table, as I did in NonzeroBasis3 though.)
Simply use searchSpan2 instead of searchSpan, mainly based on my personal preference. (Your searchSpan also need to be modified if you want to compile it. It's not hard to take it out of Compile, of course. )

Here's the compiled NonzeroBasis:

(* This line is just to tell you a truth: *)
knots = aaa; u0 = bbb;
compiledNonzeroBasis = 
 With[{coeff = (u0 - knots[[#1 + 1]])/(knots[[#1 + #2 + 1]] - knots[[#1 + 1]]) &}, 
  ReleaseHold[
    Hold@Compile[{{deg, _Integer}, {knots, _Real, 1}, {u0, _Real}}, 
       Module[{basis = ConstantArray[1., {deg + 1, deg + 1}], 
               i = searchSpan2[knots, u0] - 1},
    Do[basis[[deg + 1 - k, k + 1]] = (1 - coeff[i - k + 1, k]) basis[[deg + 2 - k, k]];
     With[{m = deg + 1 - i}, 
      Do[basis[[m + j, k + 1]] = {coeff[j, k], 
          1 - coeff[j + 1, k]}.{basis[[m + j, k]], basis[[m + j + 1, k]]}, {j, 
        i - k + 1, i - 1}]];
     basis[[deg + 1, k + 1]] = coeff[i, k] basis[[deg + 1, k]], {k, deg}];
    basis]] /. DownValues@searchSpan2]];


knots = {0, 0, 0, 0, 0, 1, 2, 3, 4, 4, 5, 6, 7, 8, 9, 10, 10, 10, 10, 10};

compiledNonzeroBasis[deg0, knots0, 2.5]; // AbsoluteTiming
(* {1.437518, Null} *)

And, if speed is really concerned, here's a optimized version of my NonzeroBasis3(Notice that a C compiler is necessary):

(* This line is just to tell you a truth: *)
u = aaa; u0 = bbb;
With[{g = Compile`GetElement}, 
  coeff[x1_, x2_] := (u0 - g[u, x1])/(g[u, x1 + x2] - g[u, x1]);
  optimizedNonzeroBasis3 = 
   ReleaseHold[
    Hold@Compile[{{p, _Integer}, {u, _Real, 1}, {u0, _Real}}, 
        With[{i = searchSpan2[u, u0]}, 
         Module[{lst = Table[0., {i + 1}, {p + 1}]}, lst[[i, 1]] = 1.;
          Do[
           lst[[j, k + 1]] = 
            coeff[j, k] g[lst, j, k] + (1 - coeff[j + 1, k]) g[lst, j + 1, k], 
            {k, p}, {j, i - k, i}];
          lst]], CompilationTarget -> "C", RuntimeOptions -> "Speed"] /. 
      DownValues@searchSpan2 /. DownValues@coeff]];
optimizedNonzeroBasis3[deg0, knots0, 2.5]; // AbsoluteTiming
(* {0.124957, Null} *)

In the function NonzeroBasis3, when I replace lst[[j, k + 1]] = (u0 - u[[j]])/(u[[j + k]] - u[[j]]) lst[[j, k]] + (1 - (u0 - u[[j + 1]])/(u[[j + k + 1]] - u[[j + 1]])) lst[[j + 1, k]] with lst[[j, k + 1]] = coeff[j, k] lst[[j, k]] + (1 - coeff[j + 1, k] ) lst[[j + 1, k]], here coeff = (u0 - u[[#1]])/(u[[#1 + #2]] - u[[#1]]) & in the Module enviroment, however, it failed. Could you tell me why?THX:) — xyz, Aug 17 '15 at 01:00
Thanks a lot:). I am not familiar with Compile, so your code is very helpful for me. — xyz, Aug 17 '15 at 04:28
For the auxiliary fuction searchSpan[], Please see my edit in here — xyz, Aug 17 '15 at 05:02
Maybe a bug. knots1 = {0, 0, 0, 0, 0, 1, 2, 3, 4, 4, 5, 6, 7, 8, 9, 10, 10, 10, 10,10}; then searchSpan2[knots1, 10] searchSpan[{2, knots1}, 10] — xyz, Aug 17 '15 at 05:16
@ShutaoTang knots1 doesn't fit the description, right? $u_0 \in [u_i,u_{i+1})$ so $u_i<u_{i+1}$. — xzczd, Aug 17 '15 at 05:28
@ShutaoTang If the last element needs special treatment, you can use something like searchSpan2[knots_, u0_] := First@Ordering[Sign[u0 - knots], 1] + If[knots[[-1]] == u0, 1, -1] — xzczd, Aug 17 '15 at 06:20
@xzczd you can use the CompileExpand function from the following answer instead of replacing DownValues. http://mathematica.stackexchange.com/a/24596/66 — faysou, Nov 10 '16 at 08:57
@faysou Actually I know (and have already upvoted) this answer for years, but was not skilled enough to understand and use that function :) — xzczd, Jan 17 '17 at 07:32
The key innovation that allowed the CompileExpand function is the Step function from Mr Wizard. — faysou, Jan 17 '17 at 13:50
@faysou Actually this elegant yet abstruse function was one of the main barrier for my understanding 囧. It took me quite a while to figure out the meaning of P = (P = … today (after using Mathematica for more than 4 years! ). — xzczd, Jan 17 '17 at 14:36

How to implement a more efficient inverse triangular recursion?

Test

Performance test

Question

Update

1 Answers1

Update